
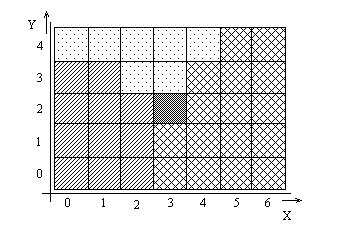
Obr. 1 Příklad vstupního obrázku
Tato práce se zabývá převodem rastrových dat do vektorové podoby. Práce je zaměřena spíše na popis algoritmu. Většina dosavadních prací o automatické vektorizaci, s nimiž jsem se měl možnost se seznámit, byla založena na použití balíku programů. Autoři těchto nástrojů většinou nezveřejňují použité algoritmy. Proto byl na základě zadání od firmy Help Service a s využitím dostupných znalostí vytvořen nový algoritmus vhodný pro vektorizaci leteckých snímků. Vstupní letecký snímek musí být předzpracován klasifikátorem oblastí.
Další výhodnou vlastností představovaného algoritmu je jeho modularita, která umožňuje rychlé přizpůsobení programu požadavkům na změnu činnosti nebo formátu dat. Další požadavky si vynutí změny pouze v části modulů, přičemž ostatní moduly mohou zůstat v původním stavu.
Jednou z činností kartografů je snaha o udržení aktuálnosti jednotlivých map. Za tímto účelem jsou prováděna nová letecká snímkování terénu a podle výsledných fotografií jsou upravovány staré mapy viz[6]. Dosud je tento typ práce většinou dělán zčásti poloautomaticky s využitím již hotových sbírek programů a zčásti ručně. Úkolem autora je prozkoumání možnosti algoritmizace jednotlivých kroků při převodu leteckého snímku do bitové mapy. Výsledkem má být úspora lidské práce při tvorbě map z leteckých snímků.
Dosavadní postupy vektorizace s nimiž autor měl možnost se seznámit nedávaly pro případ leteckých snímků uspokojivé výsledky, nebo nebyl popis algoritmu k dispozici viz. např. [3,8,9,12]. Proto byl navržen a realizován nový postup založený na topologii konečných prostorů.
Zpracování leteckého snímku probíhá v následujících krocích:
Při leteckém snímkování vzniká bitmapový letecký snímek. Tento je potřeba předzpracovat libovolným klasifikátorem např neuronovou sítí, výsledek viz na Obr. 1. Návrh klasifikátoru a výběr příznaků není součástí této práce. Hlavní požadavek kladený na vstupní data vektorizátoru je existence shluků pixelů se stejným typem obarvení.
Algoritmus vektorizace je navržen pro vyhledávání hranic souvislých oblastí. Existují v něm homogenní oblasti se stejným označením (reprezentovaným barvou tzn. číslem zapsaným v pixelu). Každé označení představuje rozhodující vlastnost vstupních dat. Např les, jezero, silnice atd. Vyhledané hranice oblastí jsou následně převáděny do vektorové reprezentace.

Popisovaný algoritmus není navržen pro hledání hran v šedotónovém obraze. Pro tuto činnost je však možné data předem předzpracovat. Hrany mohou být nalezeny nějakým hranovým detektorem, např Canny viz.[1], a jeho výstup (po prahování s hysterezí) pak již lze dále převádět níže popsaným postupem do vektorové reprezentace.
V této kapitole je popsán základ jednoduchých metod vektorizace oblastí, které vytvářejí výstupní bitovou mapu o stejné velikosti bez ohledu na topologii. Obdobná metoda je dosud implementována v Programu TopoL.
Na celý obraz je aplikován operátor, který testuje rovnost hodnot dvou sousedních pixelů. Rovnost je testována ve všech směrech 8 okolí aktuálního bodu (popř 4 okolí). Pokud dojde v některém směru nebo ve více směrech současně k nerovnosti, pak je ve výsledném binárním obrázku pixel nastaven na hodnotu 1. Jinak je roven 0. Postup je uveden na následujících obrázcích Obr. 2 a Obr. 3:
Tento postup však má podstatnou nevýhodu dvojité odezvy na každou hranu. Existují samozřejmě vylepšené varianty, které testují shodu pouze v několika směrech (pouze zprava doleva a shora dolů). Tím je sice částečně kompenzována dvojitá odezva na změnu. Ne však úplně. Problémy se projeví při výskytu osamoceného bodu na nějaké hraně. Navíc dojde k nežádoucímu posunutí všech hran v určitém směru.
Předcházející problémy vycházejí z nesprávné reprezentace hranic oblastí. Proto jsou využity výsledky topologie konečných prostorů [14].
Při pokusu o hledání hranic oblastí a jejich reprezentaci není původní bitová mapa příliš vhodná viz Obr. 4. Proto byla použita nová metoda, která zajistí mnohem lepší kvalitu detekovaných hran.
Do obrázku jsou uměle přidány nové body v rozích a sousedních hranách původních bodů viz Obr. 5. Tyto nové body pak mají speciální vlastnosti a slouží k vyjádření topologických vazeb mezi obrazovými daty. Postup rozšíření je názorně ukázán na následující sérii obrázků Obr. 4-6



Výsledná bitová mapa na Obr. 6 je rozšířena o nové body oproti původní bitové mapě. Ty popisují hrany pixelů a rohové body. Při uvedené konfiguraci již nevzniká paradox dvou přímek viz.[1 str:30].
Původní pixely představují elementy s dim 2. Hranice dvou pixelů mají dim 1 a elementy ležící v rozích pixelů mají dim 0.
Z výše uvedených předpokladů vyplývají následující omezení. Hrana, jakožto 1D útvar nemůže samozřejmě přes body s dim>1, může procházet pouze body s dimenzí <=1. K větvení hrany (uzlu) může dojít pouze u bodů s dim 0, tzn pouze v rozích dvou pixelů.
Návrh algoritmu je proveden modulárně. Při změně požadavků je možno vyměnit popř. opravit pouze několik modulů. Např. při změně GIS je potřeba upravit pouze poslední modul. Každý modul realizuje jeden průchod. Vektorizátor má 5 hlavních průchodů. Při prvních dvou jsou zpracovávána data pouze v rastrové podobě, při třetím je vytvářena vektorová reprezentace a poslední dva pracují pouze s vektorovou reprezentací. Původní rastrový obrázek má velikost [x;y].
1.Průchod - hledání hranic
V tomto průchodu jsou hledány hranice oblastí. Je vytvářen nový pomocný binární rastr (v aktuální implementaci pojmenován KDT.RAS ) s rozměry [2*x+1;2*y+1]. Jeho okraje jsou nastaveny na 1. Vnitřní body jsou nastaveny pouze za podmínky, že leží mezi dvěma body s rozdílnou úrovní jasu. Je vyhodnocován rozdíl v podélném, příčném směru a na úhlopříčkách.
| 1 | 1 | 2 |
| 1 | 1 | 2 |
| 4 | 1 | 3 |
| . | . | . | . | . | . | . |
| . | 1 | 1 | . | 2 | . | |
| . | . | . | ||||
| . | 1 | 1 | . | 2 | . | |
| . | . | . | . | . | . | |
| . | 4 | . | 1 | . | 3 | . |
| . | . | . | . | . | . | . |
(v bitové mapě jsou uloženy pouze body označené v tabulce tečkami, čísla jsou uvedena pouze pro zvýraznění korespondence s předchozím obrázkem)
2.Průchod - hledání uzlů
V tomto průchodu jsou detekovány uzly. Je vytvořena druhá pomocná bitová mapa uzlů (v aktuální implementaci pojmenován KDU.RAS ) s rozměry [2*x+1;2*y+1]. Uzel je takový bod, který má více než dva nenulové sousední body. Pro detekci uzlů je využit binární operátor podobný dilataci.
| . | . | . | . | x | . | . |
| . | . | . | ||||
| . | . | . | ||||
| . | . | . | ||||
| x | . | . | x | . | x | |
| . | . | . | . | |||
| . | . | x | . | x | . | . |
(v bitové mapě jsou uloženy pouze body označené v tabulce písmenem 'x', tečky jsou uvedeny pouze pro zvýraznění korespondence s předchozím obrázkem)
3.průchod - detekce vektorových linií
V tomto průchodu jsou počítány vektorové linie. Každá vektorová linie musí vycházet z nějakého uzlu a do nějakého (jiného) uzlu vstupovat. Jsou vytvářeny 3 další pomocné soubory, které jsou v aktuální implementaci pojmenovány BODY.BIN, UZLY.BIN a LINIE.BIN. Vyhledávání linií probíhá následujícím způsobem: Algoritmus sekvenčně prochází obrázek KDU.RAS tak dlouho až narazí na první uzel. Z něho je proveden pokus postupovat postupně všemi čtyřmi směry. Při postupu jsou hledány následníci bodů a ty jsou zaznamenáváni do interní struktury. Při postupu jsou body postupně z rastru KDT.RAS vymazávány. Takto se pokračuje až do nalezení uzlového bodu. Potom je linie tvořena seznamem lomových bodů. Počet lomových bodů je optimalizován speciálním algoritmem. Ten je založen na kritériu nejmenších čtverců odchylky optimalizované lomené čáry od čáry původní.
Z předchozího je patrné, že uvedený postup neumožňuje nalezení uzavřených kružnice bez lomových bodů. Proto je 3 průchod proveden 2x. Při druhém postupu je kterýkoliv nalezený bod v rastru KDT.RAS považován za uzlový (s řádem 2) a je postupným procházením nalezena celá kružnice. (Vše ostatní již bylo z rastru KDT.RAS při 1. průchodu vymazáno!)
Na konci průchodu jsou dále již nepotřebné rastry KDU.RAS a KDT.RAS smazány.
4.průchod - kontrola ploch
Z každého uzlového bodu je postupováno na linii, následuje nový uzlový bod. Poté vždy proti směru hodinových ručiček až bude dosaženo do počátečního bodu. Ze zadání (vzhledem k předchozím krokům) vyplývá, že graf musí být rovinný. Z toho vyplývá, že výše popsaným způsobem je vždy uzavřena kružnice.
Příklad postupu hledání (podle Obr. 7):

Nechť je výchozí bod U1 a tento uzel má obsazenu přípojku 1. Tedy je proveden krok po linii L1 do uzlu U2. Do uzlu se vstoupí přípojkou č.3. První obsazená přípojka ve směru hodinových ručiček je č.4. Po této přípojce je uzel nakonec opuštěn. Algoritmus postupuje po linii L3 do uzlu U4. Do uzlu U4 je vstoupeno přípojkou č.2. První obsazená přípojka ve směru hodinových ručiček je č.1. Výstupní linie L4 se již vrací do vstupního uzlu U1. V tomto kroku tedy plocha uzavřena a algoritmus končí.
Při tom je ovšem současně počítána velikost plochy. Je-li větší, než stanovený limit, pak jsou všechny linie, které k ní patří označeny za platné (poznámkou v uzlových bodech).
V uzlových bodech jsou poznamenávány všechny informace o postupu. Tím je zajištěno, že plocha nemůže být nalezena 2x.
5.průchod - vytváření topologické struktury
Postupuje se, podobně jako v předchozím průchodu po jednotlivých uzlech. V každém uzlu jsou příslušné nevyřazené linie topologicky spojeny dohromady.
V tomto průchodu je prováděno i tzv. slepování zbylých linií. Některé linie mohou být slepeny pouze proto, že byli jejich sousedi vyřazeni při předchozím průchodu a vznikl uzel řádu 2. Každý uzel řádu 2 (s výjimkou kružnic)- je vyhledán a vyřazen z grafu. Při vytváření linií jsou též generovány plochy. Tím nedojde k změně topologie, ale dojde pouze k citelné redukci množství výstupních dat. Nalezené a upravené linie jsou exportovány do interních struktur programu TopoL. Pouze tento krok je závislý na použitém GIS.
Na konci průchodu jsou dále již nepotřebné soubory LINIE.BIN, BODY.BIN a UZLY.BIN smazány.
V této kapitole je obsažena diskuse o nastavitelných parametrech a jejich vlivu na výstupní vektorový formát.
Program má celkem 5 parametrů:
a, Vstupní obrázek může být jakýkoliv 2,16,256 úrovňový (s paletou i bez), DMT nebo true color. (Toto omezení vychází z použití programového balíku TopoL.) Musí v něm existovat souvislé oblasti se shodným jasem.
b, Jméno výstupního bloku specifikuje cestu, kam budou ukládána vektorizovaná data. Na cílovém výstupním zařízení musí být dostatek místa pro uložení pomocných dat.
c, Minimální plocha je určována v pixelech (může být přepočítána na [ha]). Je-li zadána plocha velmi malá <1,10>, pak dojde k extrémnímu nárůstu délky vektorového obrázku.
d, Odchylka vektorové linie určuje vyhlazení linie a vyjímání přebytečných vertexů (lomových bodů). Je zadávána v jednotce bod/bod přímky. Doporučuji hodnoty od 0.1 do 0.9. Je-li zadáno příliš malé číslo, vycházejí linie kostrbaté. Naopak při vyšší hodnotě dochází ke změnám tvaru vektorizované plochy.
e, Je-li přepínač okrajových ploch sepnut, pak jsou do výstupního vektorového obrázku posílány i plochy, které sousedí s okrajem obrazovky. V opačném případě jsou uvedené plochy ignorovány a z výsledného souboru vyloučeny.
V této kapitole je diskutovéna délka výstupního souboru. Je samozřejmé, že vektorový formát představuje pouze jinou reprezentaci dat. Proto pro některé vstupní rastry a při vysokých požadavcích na přesnost musí být vektorová reprezentace delší než původní rastrová. Větší délka dat je však vyvážena podstatně větším komfortem při editaci a změnách.
Mějme šachovici o velikosti políčka 8x8 (tj 64 bodů) - tj téměř nejhorší případ. Každé políčko je ve výsledku popsáno 1 plochou. Každé políčko má 4 linie. O každou linii se dělí se sousedním políčkem. Požadovaná přesnost vektorizace je maximální.
Další výpočty se týkají délek datových struktur programu TopoL, avšak závěry jsou aplikovatelné i na jiné vektorové reprezentace:
Délka linie = 103 byte + 2 krajní body 24 byte (4x6)
Délka plochy = 71 byte
Lpl = 4*(103+24) /2 + 71 = 325 byte
Lpl je počet byte potřebný pro jedno políčko šachovnice ve vektorovém formátu. V rastrové reprezentaci byla délka dané plochy 64 byte (pro 256 barev), nebo 32 byte pro 16 barev. To znamená 5ti (nebo 10ti) násobné zvětšení objemu dat.
Vektorový formát je výrazně (co do objemu dat) úspornější až od minimální plochy 325 bodů, což odpovídá min velikosti políčka 18x18. Ovšem pro velikost plochy 1 může být velikost vektorového obrázku až 300x větší, než původního rastru. Uživatel proto musí pečlivě vážit jaké detaily ve vektorových datech potřebuje (anebo mít dostatek diskového prostoru).
V tomto článku popisovaná metoda automatické vektorizace může ušetřit mnoho práce lidem, kteří dříve museli provádět vektorizaci leteckých snímků ručně nebo poloautomaticky. V současné implemementaci je aktuální implementace schopna vektorizovat i poměrně velké obrázky i několik set MB. V blízké budoucnosti se stane součástí programového balíku TopoL a bude dostupná širšímu okruhu uživatelů. Pro použití je potřeba mít na disku dostatek volného prostoru (min 2 násobek velikosti původního rastrového obrázku) a seznámit se s vlivem parametrů na kvalitu výstupu pro danou úlohu.