Abstract

This paper describes application of modern mathematics methods in environment GIS. Consideration is devoted especially on application "common sence", neuron networking and Fuzzy and Rough set".

Abstrakt

Článek popisuje problematiku aplikace moderních matematických metod v prostředí GIS. Pozornost je zejména věnována aplikaci metod "selské logiky, neuronových sítí a Fuzzy a Rough množin".

Úvod

          Geografie je věda popisující Zemi, nebo-li věda zabývající se geosférou. Geosféra je složitý, rozsáhlý dynamický systém s řízením, s cílovým chováním a s prostorovou organizací. Geosféru tvoří dva podsystémy:

• fyzicko-geografická sféra
• antroposféra(socioekonomická sféra).

          Antroposféra je řídící systém, fyzicko-geografická sféra pak systém řízený. Geosystém se mění v čase. Máme-li za úkol modelovat vývoj geosystému za časový úsek, nabízí se v zásadě tři možnosti:

1. statické modely - zachycují momentální stav geosystému. Jde většinou o naměřené údaje, mapy, soubory informací atd.
2. kinematické modely - zachycují stav geosystému v časových intervalech (opakovaná měření apod.)
3. dynamické modely - zachycují přechod geosystému z jednoho stavu do druhého. Tyto modely nejvěrněji popisují geosféru.

Je zřejmé, že čím má být model geosféry kvalitnější, tím je zapotřebí většího množství informací (dat):

• informační - adjektivum od slova informace. Informace je údaj, směrovaná zpráva o charakteristikách, stavech systémů, procesů a jejich částí, případně množství údajů, přenesených sdělovacím kanálem za jednotku času
• systém - účelově definovaná množina (entita, soubor) prvků (částí, jednotlivých objektů) a vazeb mezi nimi, které spolu určují vlastnosti, chování a funkce systému jako celku. Prvek systému je na dané úrovni nedělitelná část. Vazba systému realizuje spojení mezi prvky systému. Vazby a prvky tvoří strukturu systému.

          Informační systém je potom systém, jehož vazby tvoří informace. Mezi prvky tohoto systému probíhá výměna informací. Výměna probíhá i mezi systémem a jeho okolím. Okolí je taktéž tvořeno množinou prvků, které sice nejsou součástí systému, ale vykazují k některým jeho prvkům vazby. Tyto realizuje vstup a výstup systému. Takto definovaný systém nazýváme otevřený. Na základě výše uvedeného je možno definovat GIS:

"Geografický informační systém je systém lidí, technických a organizačních prostředků, který provádí sběr, přenos, uložení a zpracování údajů za účelem tvorby informací vhodných pro další využití v geografickém výzkumu a jeho praktických aplikacích."

          Je tedy zřejmé, že nejvýkonnější geografické informační systémy musí obvykle disponovat mocnými nástroji na zpracování a analýzu geografických (prostorových a atributových) dat, dále pak na analýzu blízkosti a souvislosti, tvorbu a analýzu digitálního modelu terénu, geometrická měření a výpočty, případně nástroji na realizaci modelů na bázi síťové analýzy.

          Geografické informační systémy se dnes využívají zejména pro inventarizaci, správu, případně pro analýzy a modelování v rámci určitého území.

          V současné době je většina geografických modelů založena na předpokladu, že kterýkoliv daný proces lze vyjádřit matematickým zápisem nebo souborem takových zápisů. Sestavují se tak různé druhy modelů. Modely jsou přiblížením mechanismu, dle kterého fungují reálné jevy. Čím jednodušší je jev, tím snazší je formulování jeho mechanismu matematickými prostředky. K základním používaným modelům patří:

• Logické modely - ty vycházejí ze základních axiomů logiky a řídí se pravidly binární Booleovy algebry. Jejich výsledky jsou vyjádřeny jako diskrétní, resp. alternativní veličiny (pravda /nepravda)
• Deterministické modely - popisují jevy ve smyslu fyzikálních zákonů. Základním jejich předpokladem je tvrzení, že fyzikální síly řídící proces jsou známy a vše, co je požadováno, je shromáždit odpovídající data. Přesnost těchto modelů závisí na kvalitě nashromážděných dat a nedefinovaných parametrech modelu.
• Stochastické modely - popisují jevy ve smyslu fyzikálních zákonů. Na rozdíl od deterministických modelů je alespoň jedna ze vstupních veličin nebo alespoň jeden z parametrů vyjádřen jako pravděpodobnostní proměnná. Výsledky těchto modelů jsou pravděpodobnostní funkce. Vhodně kalibrované stochastické modely pak mohou vyjadřovat prognózy modelovaných jevů pomocí např. středních hodnot výsledných rozdělení.
• Optimalizační a strategické modely - jde převážně o modely založené na teorií operačního výzkumu. Do této oblasti patří řada metod a analýz založených např. na síťovém grafu, lineárním a nelineárním matematickém programování. K nejznámějším modelům patří problematika modelování dopravních sítí.

          Klasické formální metody modelování složitých nebo vágně definovaných systémů nemusí být příliš úspěšné. Tyto klasické metody byly a jsou dosud často aplikovány z důvodu, že donedávna neexistovaly formální prostředky analýzy a syntézy respektující složitost takovýchto modelů. Slibným zdrojem metod, použitelných v této oblasti, se jeví vědy, které od samého počátku pracují se složitými a obtížně popsatelnými modely (např. sociologie, predikce apod.). Tyto vědecké disciplíny přijaly systém popisu nikoliv exaktními metodami (diferenciálními rovnicemi či Booleovskými logickými vztahy), ale metodami umožňujícími slovní popis systému, např. tzv. selskou logikou či fuzzy logikou.

          V posledních cca 20 let se objevila a objevuje řada metod a idejí (jazykové modely na bázi fuzzy matematiky, Rough množin, teorie chaosu, neuronových sítí apod.), které vznikaly na základě tlaku praxe na potřeby studia a modelování složitých a vágně definovaných systémů. Úspěch těchto modelů spočívá především v tom, že se s pojmem vágnosti vyrovnaly na úrovni interpretace nových matematických teorií a nikoliv užitím "vágního formálního aparátu". Při jejich praktických aplikací se však naráží na řadu konkrétních problémů plynoucích ze skutečností, že nejsou potřebné (nebo jsou velmi malé) zkušenosti s formulací konkrétních reálných úloh pomocí těchto nových formálních nástrojů, neexistuje metodologie tohoto druhu modelování a často neexistuje ani potřebné programové vybavení. Aplikace těchto nových matematických postupů se jeví vhodná zejména pro následující oblasti:

1. Stavebnictví
   • Územní plánování
   • Dopravní průzkumy
   • Správa energetických sítí
   • Správa a užívání dopravních sítí
   • Užívání komunikací
   • Evidence nemovitostí
   • Stavební řízení
   • Problematika analýz časových řad
   • Problematika predikce investiční politiky
   • Vyhodnocování pravdivosti kvalitativních a kvantitativních informačních dat
   • Modelování dopravy a přepravních vztahů s využitím analýzy nehodovosti ve vztahu ke společensky přijatelné bezpečnosti provozu

1. Prostorová ekonomiky
   • Analýza trhu s nemovitostmi
   • Lokální strategie veřejného zájmu
   • Demografické analýzy-změny a využitelnost potencionálů
   • Topologická analýza
   • Vyhodnocování funkcí území
   • Varianty projektového řízení

1. Životní prostředí
   • Modelování spolehlivosti a efektivnosti vodohospodářských opatření k ochraně obyvatelstva a životního prostředí při extrémních situacích
   • Výzkum a modelování znečistění

Aplikace neuronové sítí

          Neuronové sítě lze prakticky použít všude tam, kde jsou k dispozici příkladová data, která dostatečně pokrývají problémovou oblast. Další možnou oblastí je modelování složitých dynamicky se měnících systémů. Jinou důležitou aplikační oblastí může být predikce a následné rozhodování. Teorie neuronových sítí nachází také uplatnění v oblasti expertních systémů. Velkým problémem klasických expertních systémů založených na pravidlech je vytvoření báze znalostí. Neuronové sítě zde představují alternativní řešení, kde reprezentace znalostí v bázi vzniká učením z příkladových inferencí. Další oblastí využití neuronových sítí může být aplikace v oblastech minimalizace účelových funkcí popisujících daný stav systému (např. minimalizace energie apod.).

          Nejznámějším a nejpoužívanějším modelem neuronové sítě je vícevrstvá neuronová síť s učícím se algoritmem zpětného šíření chyby. Tento model se používá v 80% všech aplikací neuronových sítí. Velmi známým modelem je rovněž tzv. Hopfieldova síť. Organizační dynamika Hopfieldovy sítě specifikuje na začátku pevnou úplnou topologii cyklické sítě s neurony, kde každý neuron v síti je spojen s každým, takže má všechny neurony za své vstupy. Dále všechny neurony v síti jsou zároveň vstupní i výstupní. Spoj v síti od neuronu i (i=1, ...., n) směrem k neuronu j (j=1, ...., n) je přitom ohodnocen celočíselnou sympatickou váhou wij. Hopfieldova síť má svou přirozenou fyzikální analogii. V souladu s touto analogií lze definovat energetickou funkci E(y) sítě, která každému stavu sítě přiřazuje jeho potencionální energii podle vztahu:

(1)

          Během aktivního režimu spojité Hopfieldovy sítě se tedy minimalizuje energie E ve stavovém prostoru. Z výše popsaného je zřejmé, že této vlastnosti se dá využít při heuristickém řešení jistých optimalizačních problémů, při nichž lze minimalizovanou účelovou funkci a případná omezení vyjádřit ve tvaru kvadratické formy dle vztahu (1). Porovnáním příslušné účelové funkce s energetickou funkcí se vyextrahují váhy spojité Hopfieldovy sítě ("adaptivní režim"). V aktivním režimu pak hledáme optimální přípustné řešení daného problému. Možné aplikace se nacházejí například v oblasti optimalizačních úloh realizovaných na dopravní síti.

Aplikace selské logiky

Úvod

          V praxi existují dvě různé metodologie, jak řešit praktické problémy modelování různých problémů:

• intuitivní přistup, který je charakterizován minimálními výpočty,
• formálně orientovaný postup, většinou s využitím počítačů.

          Obě dvě metodologie jsou velmi úzce propojeny. Selská logika dominuje v průběhu počátečních fází návrhu modelu systému. Je však třeba zdůraznit, že použití selské logiky je neustále nutné pro flexibilní kontrolu počítačových a jakýchkoliv jiných výsledků.

          Tradiční inženýrský přístup k řešení problému může být charakterizován následující posloupností kroků:

• je vyvinut konvenční matematický model s využitím dosažitelných teorii,
• s použitím experimentálních dat jsou identifikovány numerické hodnoty všech údajů, které jsou potřeba pro použití modelu,
• výsledný matematicky model je numericky řešen.

          Největší nevýhoda tohoto postupu je v tom, že takovýto přístup je časově náročný

a obyčejně i velmi drahý. Jeho největší výhoda spočívá v tom, že reakce modelu jsou numericky kvantifikovány. Velmi často je k dispozici konvenční model procesu, který je studován. V praxi je však velmi často potřeba řešit problémy logického charakteru

a nejenom provádět numerické výpočty. Jako příklady takových logicky orientovaných problémů je možno uvést například stanovení všech možných způsobů jak maximalizovat profit, nebo jak naplánovat experimenty, vylepšit stávající modelovaný proces atd.

          Lidské myšlení není založeno na rovnicích. Jeden z nejmohutnějších nástrojů používaný lidmi je jejich schopnost řešit problémy s pomocí selské logiky. Kvalitativní modely představují nejrozvinutější formální aparát selské logiky, který je již v praxi v současné době použitelný jako teoretické pozadí pro formalizaci selské logiky.

Kvalitativní modely

          Analýza chování modelu s využitím selské logiky zaručuje kompletnost výsledku, kde výsledkem je seznam kvalitativních scénářů. Seznam scénářů je možno použít pro generování přechodového grafu, který sumarizuje všechna možná neustálená chování. Takový přechodový graf proto může být s úspěchem použit pro soustavné testování modelovaného systému.

          Numerická matematika a statistická analýza jsou tradiční klíčové formální instrumenty, které se požívají při modelování různých procesů. Dnes je však již jasné, že jejich možnosti jsou již vyčerpány. Jako příklad je možno uvést numerická řešení diferenciálních rovnic, které jsou běžně používány k popisu studovaných procesů. Další vývoj numerických metod by měl minimální vliv na kvalitu vytvářených modelů. Z toho plyne, že pro rozvoj modelů složitých procesů je důležitější vložit dodatečné informace než rozvíjet klasické metody.

Základní pojmy kvalitativního modelování

          Předpokládejme, že existují jenom tři hodnoty a to "kladný, nulový, negativní". Kvalitativní řešení kvalitativního modelu je specifikováno tak, že jsou popsány všechny jeho kvalitativní proměnné:

X1 , X2 , .......Xn (2)

pomoci kvalitativního tripletu:

(X , DX , DDX), (3)

kde DX a DDX představují první a druhé kvalitativní derivace. Tyto derivace jsou časové derivace.

          Množina kvalitativních řešení neboli scénářů není jediný výsledek řešení kvalitativního modelu. Množina všech možných přechodů mezi těmito řešeními (scénáři) je další významný výsledek. Jestli je každý scénář reprezentován uzlem a všechny možné přechody mezi nimi jsou znázorněny orientovanými šipkami, tak výsledkem je přechodový graf. Je to orientovaný graf všech možných přechodů.

          Jakékoliv chování studovaného systému v čase je možné charakterizovat jako orientovanou cestu v přechodovém grafu. Přechodový graf je tudíž způsob, jak velmi úsporným způsobem popsat všechna možná neustálená chování studovaného systému. Jestliže jsou k dispozici on-line data studovaného systému, je možné tato měření konfrontovat s přechodovým grafem.

Základními výhodami selské logiky / kvalitativního modelování je skutečnost, že:

• není zapotřebí žádné numerické hodnoty parametru a konstant,
• množina scénářů je prokazatelně kompletní, tj. nemůže existovat nějaké neustálené chování, které není na seznamu.

          Kvalitativní modelování, logika a optimalizace neeliminují konvenční přístupy k optimalizaci modelu. Z hlediska optimalizace je nejobtížnější problém vývoje takových metod, které by umožnily identifikaci scénářů, které kvantitativně neexistují. Dosud však není jasné, jak by se tato eliminace mohla udělat. Je však třeba konstatovat, že by tento eliminační algoritmus byl velmi užitečný. Rozděloval by nagenerované scénáře do tři skupin a to na ty, které určitě kvantitativně existují, na ty, které kvantitativně určitě neexistuji a na ty, o kterých to není možné konstatovat.

Jednoduchý příklad kvalitativního modelování

          V rámci jednoduchého příkladu budou nyní nastíněny možnosti kvalitativního modelování za použití aparátu "selské logiky".

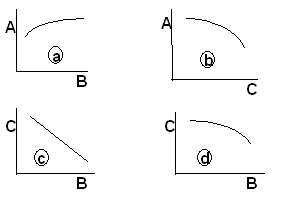Podívejme se nyní na jednoduchý příklad. Mějme proces, který je reprezentován třemi proměnnými pojmenovanými A, B, C. Tento proces není jednoznačně identifikovaný a proto je možný popis dvěma modely. Na této vlastně "jakési černé skříňce" bude demonstrována idea bezrovnicové identifikace. První model M1 je popsán vztahy a, b, c (viz. obr. 1). Druhý model M2 je reprezentován vztahy a, b, d (viz. obr. 1).

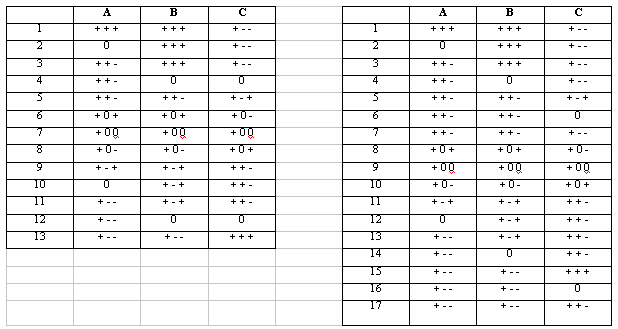
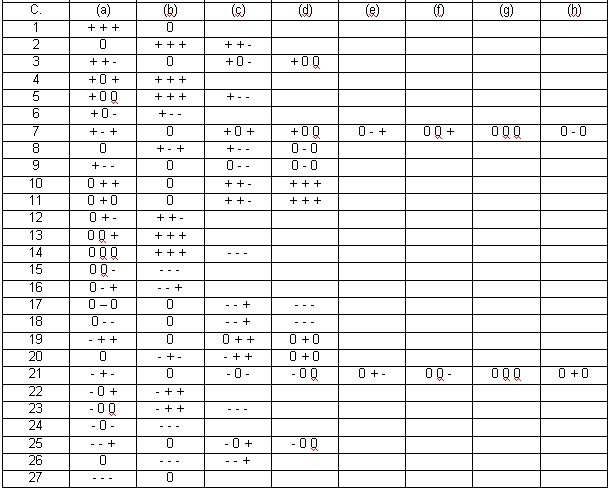
Oba dva modely mohou být řešeny, to znamená, že všechny kvalitativní popisy, které jsou slučitelné s korespondujícími modely jsou určeny. První model M1 má 13 kvalitativních scénářů (viz tabulka 1). Druhý model má 17 kvalitativních scénářů (viz tabulka 2).

Obr. 1 Grafická interpretace proměnných modelů M1 a M2

Tab. 1: Kompletní seznam všech scénářů pro model 1 Tab. 2: Kompletní seznam všech scénářů pro model 2

Na příklad, první scénář prvního modelu

(A, DA, DDA) (B, DB, DDB) (C, DC, DDC)                      (4)

(+ + + )            (+ + + )            (+ - - )

ukazuje, že kvalitativní chování veličin A a B je stejné. Obě první derivace v čase (dle 3) jsou kladné (příslušné proměnné rostou). Obě dvě druhé derivace jsou také kladné. Proměnná C však klesá, neboť první derivace je záporná. Scénáře, které jsou základní pro oba modely jsou dáno vztahem 5:

(5)

Čísla scénářů jsou převzaty z tabulky 2. V základě vzato, tyto scénáře nemohou být využity k rozlišení mezi modely a nejsou tak užitečné pro náš záměr.

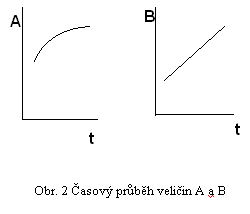          Na přiblížení tohoto problému k reálné situaci, předpokládejme, že je možné měřit (či jinak zjistit) pouze hodnoty veličin A a B. Proměnná C není měřitelná. Obrázek 2 ukazuje dva časové průběhy veličin A a B. Naskýtá se však otázka, zda je možné rekonstruovat chování veličiny C jako funkce v závislosti na čase pokud grafy na obr. 2 představují kvantitativní hodnoty měření. Tyto kvantitativní měření budou pak využity na potvrzení nebo zamítnutí modelů M1 nebo M2.

Kvantitativní grafy na obr. 2 mohou být kvalitativně degradovány. Výsledkem je kvalitativní popis obr. 2:

(6)

Tento popis pokrývá scénáře číslo 4 modelu M1 (viz tab. 1) a scénáře 4 modelu M2

(viz tab. 2). Nicméně zde jsou dva rozdílné kvalitativní popisy proměnné C pro dané případy:

(7)

Je jasné, že první derivace je záporná a že druhá derivace je buď rovněž záporná (druhý model), nebo je rovna nule (první model).

          Velmi často záznamy pozorování (měření) jsou tak nepřesné, že není možné rozlišit lineární a nelineární model. V takovém případě i když proměnná C bude měřitelná, není možné identifikovat správný model. Jinými slovy, žádný z obou kvalitativních modelů

(obr. 1) nemůže být porovnáním daných pozorování (měření) (viz obr. 2) zamítnut.

          Množina kvalitativní scénářů není pouze výsledek kvalitativního modelování. Množina možných změn (přechodů) nad množinou scénářů je další velmi zajímavý výsledek. Jestliže každý scénář je reprezentován uzlem a všechny stavy jsou graficky reprezentované orientovanou hranou mezi korespondujícím párem scénářů, pak výsledkem je orientovaný síťový graf všech možných stavů. Časový průběh studovaných systémů může být charakterizován cestou v přechodovém grafu. A přechodový graf je tak zhuštěný popis všech možných neustálených stavů v závislosti čase.

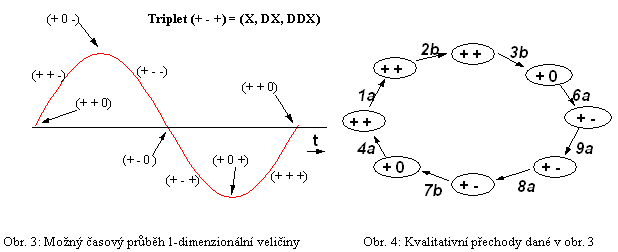
          Obrázek 3 ukazuje jednoduchý příklad 1-dimensionální změny okolo střední hodnoty s možnými stavy dle obr. 4. Stavová čísla z grafu 4 korespondují se stavy v tabulce 3 (stav 3b znamená řádek 3, sloupec b).

          Při návratu k modelům M1 a M2 je zřejmé, že obr. 5 reprezentuje 3-dimensionální stavové možnosti pro první model M1. Na příklad, scénář 6 (viz tab. 1) může přejít pouze do scénáře 1 a ten pouze do scénáře 2 atd.

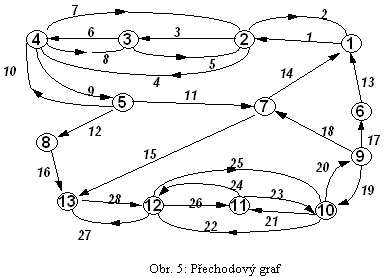
          Kvalitativní degradace kvantitativních měření proměnných A, B a C může být vždy popsána cestou (nebo množinou cest) v přechodovém grafu. Na příklad cesta z 9 .. do .. 10 .. do .. 9 (viz obr. 4) může modelovat jisté oscilace v chování popsaném následující časovou sekvencí kvalitativních scénářů (viz také tab. 1)

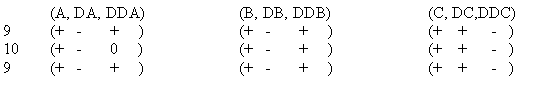
Přechodový graf je velmi užitečný nástroj pro širokou oblast plánování. Časové sekvence scénářů jsou vždy prezentovány orientovanou cestou v stavovém grafu.

Tab. 3: Seznam všech jednorozměrných přechodů dle obr. 3

Aplikace Fuzzy množin

          Fuzzy logika slouží pro popis jevů, které lze jen obtížně popisovat klasicky, resp. jevů s "nejasnými hranicemi. Fuzzy logika je považována za jednu za jednu z nejrychleji se rozvíjejících teorií i technologií 90. let.

Proces sestavení Fuzzy modelu lze popsat ve třech bodech:

1. Fuzzyfikace - kdy ne zcela jasné vstupní hodnoty jsou převedeny na neurčité hodnoty
2. Vyhodnocovací kriteria - na základě daného kriteria jsou ze vstupních neurčitých hodnot vypočteny výstupní hodnoty
3. Defuzzyfikace - výstupní neurčité hodnoty jsou převedeny na výstupní veličinu

          První krok zahrnuje definici rozmezí hodnot, pro které jsou funkce příslušnosti ("fuzzy množiny") platné. Rozmezí určuje většinou aplikační pracovník při sestavování modelu. Toto rozmezí hodnot může být následně i pozměněno. Druhý krok zahrnuje definici pravidel a kriterií, jež popisují vztah mezi vstupními a výstupními proměnnými vyjádřený pomocí funkce příslušnosti. První a druhý krok představují velmi jednoduché akce. Jde vlastně o rozložení problému na množství primárních kriterií a množství rozhodnutí. Jednou z předností neurčité logiky je, že pro uspokojivé řešení problému (řešení, jež je použitelné v rámci povolených tolerancí na výstupu modelu) není nutno definovat rozhodnutí pro všechny kombinace možných kriterií. Je možné obdržet přijatelné řešení na základě definice pouhé části z možných kriterií.

          Defuzifikace představuje proces při kterém se z výsledné fuzzy množiny výstupní veličiny po inferenci určuje např. jedna konkrétní hodnota výstupu. Existuje několik metod defuzifikace, např. Metoda centroidů, střední hodnota součtů, metoda prvního maxima, metoda středu maxima, metoda výšek

          Neurčitá logika je jednou z mnoha nově vznikajících a používaných technologií. Mezi její nejzajímavější aplikační oblast patří převážně oblast expertních systémů.

Význam použití kvalitativních modelů pro praxi

          Umělá inteligence je generátor širokého spektra idejí, algoritmů a metodologií, které mohou být úspěšně použity pro řešení problému z oblasti modelování, řízení. Jak již bylo konstatováno, jakékoliv neustálené chování musí být vždy reprezentováno např. nějakou cestou v přechodovém grafu. Tento fakt například dovoluje identifikovat podezřelé chování modelu (pravděpodobně poruchu) jsou li kvalitativní degradované on-line data (měření) k dispozici, mělký kvantitativní model může být použit jako sub-algoritmus v samoučícím se regulátoru. Predikováno může být i dynamické chování některých neměřitelných veličin.

          Základní výhoda kvalitativní analýzy je její nenumerická orientace a to, že množina řešení je vždy nadmnožina inženýrsky rozumných řešení. To znamená, že nic "rozumného" nemůže byt přehlédnuto, například při optimalizaci, za předpokladu, že je k dispozici dobrý kvalitativní model.

Použitá literatura

[1] Skýva L.: Energeticky optimální řízení dopravních systémů, Nadas, 1987

[2] Dohnal M.: A Methodology for Common-sence model development, Computers in Industry, 16, 141-158, 1991

[3] Voženílek V.: Počítačové modely a GIS, GIS Ostrava 97, 1997

[4] Zimmermann H. J.: Fuzzy set theory, Kluwer Academic Publisher, 1996

V článku jsou využity výsledky řešení projektu podporovaného Grantovou Agenturou České Republiky GAČR 103/98/0749.