Použití lineárního referenčního systému pro popis dopravních sítí

Petr Cenek,
Katedra dopraných sietí
Žilinská univerzita, Fakulta riadenia a informatiky
Velký Diel
010 26 Žilina, Slovenská republika
tel: + 421 89 5651015, fax: + 421 89 5651015
e-mail: petr@frdsa.utc.sk

The data on transportation networks can be used for analytical evaluations, optimisation tasks or visualisation of networks. Each of those purposes demand different model of a network. A general model of a network uses a linear referencing system, which allows to use a common description of nodes and edges of a network without regarding their geometrical or geographical characteristics. The whole model of a network then uses linear reference layer, geometrical layer and reference methods layer.

The paper shows basic problems of building such a data model and our own experience with the implementation of linear referencing system n for optimisation and simulation models in railway applications.

Správa údajů o dopravních sítích, vypracování analýz, řešení optimalizačních úloh na sítích a zobrazování sítí vyžaduje rozdílné vlastnosti modelů sítě. Pro sjednocení pohledu na modelovanou síť se proto používá lineární referenční systém, který dovoluje jednotný popis uzlů a úseků sítě bez ohledu na jejich geometrické anebo geografické charakteristiky. Celý model sítě potom obsahuje kromě tohoto referenčního popisu i vrstvu geometrickou a vrstvu přidružených atributů anebo metod.

Příspěvek ukazuje základní problémy budování a zkušenosti s vlastním použitím lineárního referenčního systému při budování optimalizačních a simulačních modelů dopravních systémů zejména pro aplikace v železniční dopravě.

Údaje jsou nejnákladnější složkou budovaných informačních systémů a proto je třeba jejich pořizování a ukládání věnovat patřičnou pozornost. Je asi přirozeným požadavkem, že jednou pořízené údaje se budeme snažit využít pro všechny řešené úlohy a vyhneme se tak nákladnému opakovanému pořizování dat.

Na druhé straně si však musíme uvědomit, že každá řešená úloha může vyžadovat zcela odlišný typ údajů a také jiný způsob přístupu k informacím. Například pro editování potřebujeme často měnit obsah a počet záznamů a budeme proto potřebovat dynamickou strukturu, která dovolí snadné editování a zápis zpracovávaných informací. Naopak při řešení optimalizačních úloh potřebujeme obvykle rychlé vyhledání určité informace a v takovém případě bude výhodné použít statických údajových struktur, které budou předem uspořádány tak, aby usnadňovaly vyhledávání informací.

Jiným hlediskem je obsah informací o sítích. Opět si musíme uvědomit, že budeme údaje používat pro nejrůznější účely a každá úloha bude vyžadovat jiné údaje z hlediska jejich obsahu. Pokud budeme zpracovávat údaje o sítích musíme v každém případě pracovat s informacemi o topologii sítě, jinak bychom měli k dispozici pouze jakýsi seznam informací, který by však nereprezentoval požadovanou dopravní síť. Topologie sítě udává vztahy mezi uzly a úseky sítě (incidenci neboli přilehlost uzlů a úseků sítě).

Dalším typem údajů může být popis vlastností (atributů) jednotlivých prvků sítě. Při popisu těchto atributů často používáme jejich vztahu k úsekům sítě a můžeme určit, že například na vzdálenosti 5,2 km od začátku silničního úseku je můstek, na 16 km je ve vzdálenosti 5 metrů od komunikace postavena budova celnice a mezi 18 a 20 kilometrem je omezena rychlost jízdy na 50 km/hod. Všechny tyto vlastnosti byly vztaženy na vzdálenost od začátku úseku a jsou tedy definovány lineárním souřadným systémem.

Posledním typem údajů, které potřebujeme zejména pro zobrazování sítí jsou údaje o geometrickém anebo geografickém uspořádání sítě. Jsou to tedy údaje o směrovém a výškovém vedení komunikací (obloucích a sklonech komunikací), které nám dovolují vykreslit dopravní síť tak, jak ji máme zobrazenu např. na mapě a případně můžeme tyto údaje využít v některých analytických úlohách (při výpočtu dynamiky jízdy apod.)

Všimněme si, že jsme popsali tři vzájemně zdánlivě nezávislé skupiny údajů o dopravních sítích. Je zřejmé, že také musíme vhodným způsobem definovat vzájemné souvislosti mezi jednotlivými typy údajů, což pro některé údaje bude úloha triviální, pro některé bude třeba vzájemné vazby explicitně určit. V dalších částech ukážeme model dopravní sítě a údaje potřebné pro jejich popis a pro řešení určitých typů úloh na sítích se zvláštním zřetelem k využití lineárního referenčního systému.

 

Dopravní síť může představovat libovolnou infrastrukturu, která bude mít charakter sítě a skládá se tedy z uzlů propojených úseky sítě. V tomto smyslu můžeme všechny další úvahy považovat za platné i pro obecné typy sítí jako jsou například rozvodné sítě plynu nebo elektrické energie, sítě telekomunikační a počítačové a do určité míry i sítě služeb, které sice nemají hmotný charakter, ale mohou být zadávány a analyzovány stejnými prostředky jako ostatní sítě (může se jednat například o sítě autobusových nebo vlakových spojů, sítě MHD apod.) Dopravní sítě tak mohou sloužit jako modely reprezentující množství reálných systémů, ve kterých mohou probíhat výrobní, skladovací anebo dopravní činnosti.

Model dopravní sítě tedy obsahuje uzly (které představují zdroje, výrobny, sklady, prodejny) a úseky (které definují možnost přepravy mezi uzly sítě). Dopravní síť (infrastruktura) je pevnou částí dopravního systému. Pohyblivou část dopravního systému představují dopravní proudy mezi jednotlivými uzly, které jsou určeny svými intenzitami (počty prvků přepravených za jednotku času).

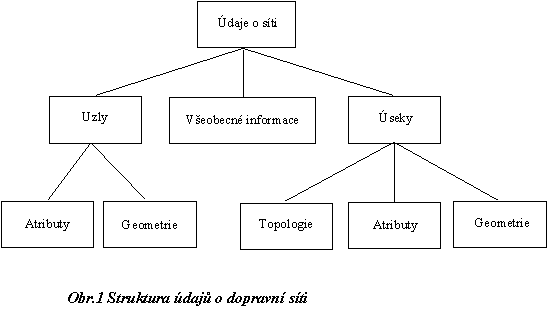
Údaje o dopravní síti můžeme rozdělit na údaje obecné, údaje o uzlech a o úsecích sítě. Pro řešení většiny optimalizačních úloh potřebujeme především údaje o úsecích, které můžeme rozdělit na:

Takto jsme rozdělili informace z hlediska jejich významu pro řešení různých typů úloh.

V kapitole 2 jsme ukázali informace, které může obsahovat model dopravní sítě, a možné interpretace resp. různá možná použití těchto informací. Pro takové obecné a různorodé použití je třeba, aby údajová struktura popisující dopravní síť obsahovala všechny potřebné informace a byla přitom zcela univerzální. Těmto požadavkům vyhovuje lineární referenční systém.

Základním prvkem lineárního referenčního systému je lineární systém (linear datum), který je zcela abstraktní strukturou a reprezentuje nejobecnější údaje o dopravní síti. Lineární systém podle definice představuje “… soubor objektů, které slouží jako základ pro umístění lineárního referenčního systému v reálném světě, definuje vztah databázové reprezentace k reálnému světu a poskytuje prostor pro transformace mezi různými referenčními systémy a geografickými reprezentacemi. Lineární systém se skládá ze základních sekcí (anchor sections) a základních bodů (anchor points), které leží v místě spojení sekcí anebo na konci sekcí. K lineárnímu systému nejsou přiřazeny žádné atributy”.

Tuto snad příliš teoretickou definici se pokusíme ilustrovat obrázkem 2.

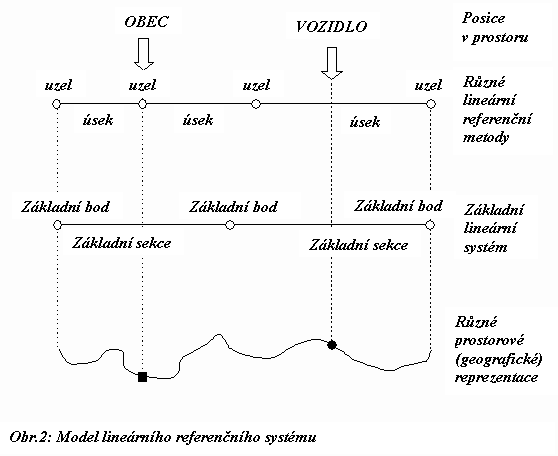
Význam jednotlivých vrstev se pokusíme objasnit na příkladu. Lineární systém slouží jako obecná reference pro jakýkoliv údaj o prvcích dopravní sítě. V příkladu uvedeném na obrázku 2 tvoří základní lineární systém dvě základní sekce, které mohou odpovídat například úsekům komunikace ze Žiliny na hranici a z hranice do Ostravy. Vrstva referenčních metod má 4 uzly a 3 úseky sítě, které odpovídají městům na cestě do Ostravy a reprezentují údaje o silniční síti. Konečně geografické vrstva obsahuje údaje potřebné pro zobrazení sítě, které mohou být zcela nezávislé na ostatních vrstvách. Jedinou podmínkou je, že musíme zajistit jednoznačné určení vztahů mezi údaji na všech vrstvách prostřednictvím základního lineárního systému. Pro zobrazení potom můžeme použít například mapové podklady v  různých měřítkách anebo schematický náčrt. Pokud zachováme požadované jednoznačné vztahy vzhledem k základnímu lineárnímu systému, dopravní síť se vždy správně zobrazí.

Podobně můžeme definovat i více vrstev referenčních metod. Nad základním systémem můžeme například definovat uzly a úseky sítě jak bylo naznačeno na obrázku, které mohou představovat hrubý model silniční sítě mezi městy Žilina a Ostrava. Stejně tak můžeme vytvořit druhou referenční vrstvu, která bude popisovat autobusové linky ve směru Žilina-Ostrava a kde budou uzly představovat zastávky autobusu a úseky sítě budou silniční úseky mezi zastávkami.

Lineární referenční systém bude užitečný zejména při správě údajů o sítích v GIS. Na našem pracovišti používáme modely sítí především pro omezený okruh aplikací v optimalizačních a simulačních úlohách a proto bude náš pohled na problém trochu odlišný. Základní myšlenka využití lineárního souřadného systému pro popis dopravních sítí je však užitečná pro všechny aplikace a proto ukážeme alespoň některé problémy a jejich řešení pomocí lineárního souřadného systému.

 

Při popisu vlastních zkušeností budeme raději používat pojem lineární souřadný systém, protože při řešení optimalizačních a simulačních úloh nedodržujeme úplné uspořádání vrstev tak, jak je popisováno pro lineární referenční systémy. Na druhé straně třeba přiznat, že používané modely jsou zaměřeny poněkud jednostranně na optimalizační a simulační výpočty a proto je i paleta řešených problémů poněkud jednodušší. Při plném využití údajů i pro údržbu údajů o síti může být opodstatněné použití lineárního referenčního systému v plném rozsahu. Výhody a v některých případech nutnost použití lineárního souřadného systému můžeme ukázat na několika praktických úlohách.

Při zobrazování stavu dopravního systému potřebujeme nakreslit dopravní síť a okamžitou polohu vozidel na síti (například rozmístění vozů v železniční stanici). Při umísťování vozů v kolejišti musíme respektovat lineární souřadnice, tzn. od které souřadnice (vzdálenosti) po kterou je kolej obsazena vozem a tam vůz nakreslit. Tím můžeme věrně zobrazit obsazení kolejiště a současně nakreslíme vůz vždy ve správné poloze na koleji bez ohledu na způsob zobrazení kolejiště (přesný obraz kolejiště můžeme například zaměnit schematickým nákresem a při zachování výše uvedeného postupu budou vozy vždy správně umístěny na koleji i ve schematickém nákresu).

Jiným problémem je samotné zobrazení kolejiště a vozů. Kolejiště je totiž typicky velmi dlouhé a rozteče kolejí jsou poměrně malé vzhledem k jejich délce. Při proporcionálním zobrazení bychom tedy dostali obraz, na kterém nemůžeme jednotlivé koleje rozlišit, tím méně bychom dokázali zobrazit vozy stojící na kolejích. Lineární souřadný systém nám nabízí prostředek, jak problém řešit. Jednu průběžnou kolej zvolíme za osu kolejiště a všechny důležité body kolejiště potom budeme zadávat ve vztahu k této ose. Při použití lineárních souřadnic to bude vzdálenost na ose kolejiště a vzdálenost od osy. Zvětšení roztečí mezi kolejemi potom snadno provedeme vynásobením vzdálenosti od osy vhodným koeficientem.

Konečně další úlohou, která může s výhodou využít lineární souřadný systém, je zobrazování “heterogenní” dopravní sítě. Pod tímto pojmem můžeme rozumět například zobrazení dvou železničních stanic a trati spojující obě stanice. Zřejmě budeme chtít zobrazit podrobně kolejiště v obou stanicích (abychom tam mohli rozeznat jednotlivé vlaky případně vozy), zatímco vykreslení trati mezi oběma stanicemi může použít zobrazení, ve kterém budou vzdálenosti kresleny v jiném měřítku (1 km ve stanici bude zobrazen stejnou délkou jako např.10 km trati). Takové zobrazení potom umožňuje současné zobrazení obou stanic i dlouhé trati mezi nimi v jediném obrazu. Samozřejmě, že i zobrazení vlaků bude odlišné ve stanicích a na trati mezi stanicemi. řešení jsme opět dosáhli použitím lineárního souřadného systému, kdy souřadnice (vzdálenosti) jsou zadávány v odlišných měřítkách pro různé části obrazu.

Vidíme, že lineární souřadný systém je zcela přirozeným způsobem popisu dopravních sítí i z hlediska potřeb různých aplikací. Podobně jako jsme ukázali jeho využití při zobrazování stavu dopravního systému, mohli bychom podobné potřeby lineárních souřadnic popsat i v úlohách správy sítí, případně v jiných aplikacích.

 

Lineární souřadný systém je významnou myšlenkou, na které jsou založeny aplikace GIS v dopravě. Jedná se o důležitou oblast využití GIS, o čemž svědčí i fakt, že se pro tyto dopravní aplikace používá zvláštní označení GIS-T. Zájemce o podrobnější informace si dovoluji odkázat na literaturu [2] a [3], kde je celá problematika lineárního referenčního systému popsána mnohem podrobněji. Ve svém příspěvku jsem se snažil ukázat vlastní zkušenosti z modelování dopravních sítí, které vedly k podobným poznatkům jako je vytvoření a používání lineárního referenčního systému v dopravních aplikacích.

Na příkladu jsem ukázal, že použití lineárních souřadnic je v řadě úloh celkem přirozené a dovoluje vyřešit množství různých problémů s popisem stavu dopravního systému a jeho zobrazením. Na rozdíl od lineárního referenčního systému však jsou námi použité údajové struktury poněkud jednodušší a základní lineární systém nahrazují přímo vrstvou topologickou, kde jednotlivé prvky základního systému (základní sekce a základní body) jsou nahrazeny uzly a úseky sítě. Toto zjednodušení dovoluje zrychlit zpracování, snížit paměťové nároky na popis dopravní sítě a v neposlední řadě je takový model i srozumitelnější pro běžného uživatele. Uvedená zjednodušení proto považuji za přijatelná a správná, pokud model dopravní sítě používáme pro omezenou třídu aplikací. Na druhé straně tento postup omezuje univerzálnost použití modelu a proto je třeba zvážit, zda při budování obecného modelu dopravní sítě, který by měl sloužit i jiným účelům, je možné vystačit se zjednodušeným modelem lineárního souřadného systému anebo bude třeba použít všechny vrstvy lineárního referenčního systému.

[1] Cenek,P., Klima,V., Janáček,J.: Optimalizace dopravních a spojových procesů. Edičné stredisko VŠDS, Žilina, 1994

[2] Fletcher,D. a kol.: The Case for a Unified Linear Reference Systém. URISA, Journal of the Urban and Regional Information Systems Association, Vol.10, No.1, 1998

[3] Duecker,K., Butler,A.:GIS-T Enterprise Data Model with Suggested Implementation Choices. URISA, Urban and Regional Information Systems Association, Vol.10, No.1, 1998