Prostorové datové struktury a jejich použití k indexaci prostorových objektů
Jaroslav Pokorný
MFF UK
Katedra softwarového inženýrství
Malostranské nám. 25
118 00 Praha 1
Tel.: +420 2 2191 4265 Fax: + 420 2 2191 4323
e-mail: pokorny@ksi.ms.mff.cuni.cz
Abstrakt
Reprezentace prostorových dat umožňující realizovat prostorové dotazy vyžaduje použití nových datových struktur. Tyto struktury umožňují indexovat prostorové objekty tak, aby bylo možné uvažovat topologii prostorových objektů. Aplikace databází prostorových objektů, např. v geografických informačních systémech (GIS), klade na prostorové datové struktury požadavek jejich jednoduchého zobrazení do stránek na vnější paměti. Většina diskutovaných datových struktur je založena na stromech. Cílem článku je podat přehled takových datových struktur a nastínit jejich rozvoj a perspektivy.
Abstract
Representation of spatial data enabling us to proceed spatial queries requires an application of new data structures. These structures make it possible to index spatial objects and to support spatial operations. Such operations deal with a topology of objects considered. Applications of spatial databases, e.g. in Geographic Information Systems (GIS), put a requirement on associated data structures to map them easily to pages of an external memory. Most of considered data structures are based on trees. This paper is a survey of such data structures. The goal is also to outline their development and usage in various areas.
1. Úvod
Prostorová data popisují prostorové objekty, jako jsou body, linie, oblasti, mnohoúhelníky, případně objekty složené z jednoduchých objektů, povrchy, ale i objekty vyšších dimenzí. Prostorová data mohou dokonce zahrnovat časovou složku. Pomocí prostorových objektů se popisují objekty reálného světa v mapách (města, okresy, státy), v systémech typu CAD (součástky, domy, obdélníky VLSI obvodů) a v mnoha dalších aplikacích založených na obecnějších, multimediálních databázích. Prostorová data představují jednu z datových komponent geografických informačních systémů (GIS) a jejich organizace má bezprostřední vliv na manipulaci a analýzu těchto dat.
Z pohledu databázové technologie můžeme přijmout pojem modelu prostorových dat. Pak výše zmíněné prostorové objekty jsou základem vektorového modelu prostorových dat. Pro úplnost dodejme, že GIS používají další model prostorových dat, jako je rastrový model. Někdy se hovoří o databázích obrázkových dat. Tyto databáze kladou menší důraz na analýzu dat. Tato neanalyzovaná data jsou typicky reprezentována v nějakém rastrovém formátu.
Cílem modelování prostorových dat je zajistit vhodným způsobem možnost pracovat se sousedstvím prostorových objektů a jejich konektivitou. Tyto topologické rysy jsou důležité pro zpracování dat např. v GIS, kde se řeší prostorové dotazy jako
“Najdi označení všech silnic, které procházejí Ostravou”. (D1)
Je i intuitivně zřejmé, že vektorový model je “topologický” z hlediska uvedeného dotazu více, než třeba rastrový, kde žádné topologické vztahy nejsou reprezentovány. Nicméně, jak skutečně reprezentovat vektorová data? Většina GIS je ukládá do proprietárních datových struktur tak, že jsou uloženy body, linie a oblasti, a to většinou v samostatných datových strukturách. Spojovacím elementem jsou identifikátory (Id) prostorových objektů.
Není nesnadné si představit dané struktury jako relační tabulky, které však ne vždy jsou vhodné pro realizaci uživatelských požadavků. Účelem vhodného výběru datových struktur je umožnit efektivní vyhodnocování prostorových dotazů, mezi něž patří např. dotaz na obsah dané oblasti, dotaz na průnik dvou oblastí, dotaz na nalezení nejbližších sousedů objektu apod.
Připomeňme, že GIS využívají modelu dat i pro takovou funkcionalitu, jakou je vizualizace abstrakce reálného světa, či podpora geometrických transformací, změn zobrazení apod.
Zdá se, že uvedený způsob reprezentace prostorových objektů sice umožňuje pracovat s topologickými vztahy, ovšem za značnou cenu. Mnohem vhodnější je použít další, pomocné struktury, které přímo reprezentují topologické vztahy a skutečné prostorové objekty tvoří až druhou vrstvu. Hovoříme pak o metodách prostorové indexace a o odpovídajících datových strukturách jako o prostorových datových strukturách (PDS). Výhodou prostorové indexace je, že ji lze použít nejen nad vektorovými daty, ale i nad rastrovými a obrázkovými.
Ani prostorová indexace ovšem ještě zcela neřeší vyhodnocení dotazu D1. GIS totiž vedle prostorových dat používá i data formátovaná (atributy), poskytující alfanumerické či časové hodnoty, nebo modelující různé vztahy. Tato data mohou být snadno reprezentována např. pomocí tabulek relační databáze s explicitní vazbou na prostorové objekty pomocí Id. Obecněji je možné prostorový objekt chápat jako integraci grafické a datové složky.
Příznačné pro prostorovou indexaci je, že nelze přímo použít PDS známé z indexace běžných formátovaných databází. Např. B-strom, vhodný pro indexaci primárního klíče, případně libovolného jiného atributu tabulky, není dostačující pro prostorová data, která jsou vícerozměrná. Použijeme-li přímo nějaké vícerozměrné PDS, jako vícerozměrnou mřížku, vícerozměrné B-stromy apod., dostaneme se sice do vícerozměrných prostorů, nicméně nepřekonáme skutečnost, že tyto metody byly navrženy hlavně pro vícerozměrné a nikoliv prostorové dotazy. Prostorové dotazy, jako např. na nejbližší sousedství a průnik objektů, jsou vícerozměrnými variantami klasických metod (lze-li je vůbec použít) vyhodnocovány značně neefektivně. Dalším problémem je, že uvedené metody byly navrženy pro data reprezentující body v prostoru. Ne vždy však lze prostorový objekt reprezentovat pomocí bodů.
PDS tedy poskytují samostatnou, speciální oblast výzkumu, která za posledních 15 let zaznamenala prudký rozmach. Většina PDS a jejich variant se objevila ve druhé pol. 80. let. Existuje jich dnes několik desítek. Ne všechny jsou vhodně implementovatelné. Nesmíme totiž zapomínat, že každá datová struktura v prostředí rozsáhlých dat musí byt efektivně zobrazena do prostředí diskových stránek. Ne každá PDS je vhodná pro všechny typy prostorových dotazů. Měřit lze nejen prostorové nároky na PDS, ale i složitost jednotlivých operací (INSERT, DELETE, UPDATE), které jsou implementovány pomocí mnohdy dost spletitých algoritmů. Různé verze těchto algoritmů daly vzniknout mnohdy samostatným PDS. Dvě strukturou stejné PDS tedy mohou byt odlišné v pojetí svého chování. Samostatnou operací je počáteční vybudování struktury s dané množiny dat (operace BUILD). To nastává často při inicializaci struktury v rámci nějaké aplikace, nebo např. v okamžiku tvorby dočasného indexu, tak jak je tomu u klasických databází.
Otázkou je, jak dynamické uvažovat aplikace pro danou PDS. Můžeme předpokládat takové aplikace, kde aktualizační operace nejsou tak časté a hlavní důraz je kladen na vyhodnocení prostorového dotazu. Mezi ně patří i většina GIS.
V 90. letech se objevily další aplikace PDS, jako např. zpracování obrazů. Znázorníme-li vlastnosti obrazu jako vektor v vícerozměrného prostoru (feature vector), pak lze řešit problém podobnosti obrazů jako problém nalezení nejbližších sousedů okolí koncového bodu v. Protože dimenze takových vektorů může být vysoká, uplatní se některé speciální metody odlišné od metod používaných ve 2-3 dimenzích.
Inspirativní zdroje pro PDS pocházejí z dávnověku informatiky. Patří sem zejména:
Tyto metody byly určeny hlavně pro práci s objekty ve vnitřní paměti. V článku se zaměříme na PDS podporující prostorovou indexaci objektů na diskových pamětech. Navážeme tak na článek [Po99], který poskytuje vysvětlení řady základních pojmů, jako jsou prostorové dotazy, reprezentace prostoru a další. Pro zájemce o hlubší popis PDS lze doporučit práce [Sa90a], [Sa90b], [ Sa95] a [GG98]. PDS jsou též přehledově zpracovány jako kapitoly v knihách [Be97] a [Su98]. Kapitola o PDS je k nalezení též ve skriptech [Po97].
V sekci 2 se zaměříme na otázky reprezentace prostoru a rozdělíme podle toho jednotlivé PDS. Rozlišíme transformační přístup a přístupy pomocí nepřekrývajících se oblastí a pokrývajících oblastí. Těžiště článku tvoří sekce 3 pojednávací o PDS pro indexaci bodů a sekce 4 obsahující informace o nejdůležitějších PDS pro indexaci obecných objektů využívajících pokrývající oblasti. V závěru jsou uvedeny některé perspektivy vývoje PDS.
2. Reprezentace prostoru a prostorových objektů
U PDS pojednávaných v tomto článku je zdůrazňováno, aby byly rozumným způsobem implementovatelné pomocí stránek umístěných na vnější paměti. To může být, i přes určitou jejich atraktivnost, problém. Tak jako nemůže ve formátovaných databázích být pro indexaci dat přímo využitelný binární vyhledávací strom, tak nemůže být u databází prostorových objektů přímo využitelný (jak uvidíme dále) např. k-d-strom. Cílem databázového zpracování je totiž i minimalizace přístupů na vnější paměť.
PDS lze rozdělovat podle různých kritérií. Jedno z nich souvisí s pojetím výchozího prostoru P, ve kterém jsou prostorové objekty umístěny. PDS tak lze rozdělit do dvou kategorií. První z nich transformuje prostorové objekty do prostoru jiné dimenze, kde se jeví jako body. Ve druhé kategorii je prostor P rozdělen (nebo je dynamicky rozdělován) do podprostorů. Ty se, vzhledem k jejich potenciální reprezentaci na vnější paměti, někdy nazývají kapsy (angl. buckets).
Podprostory mohou být reprezentovány všechny, i když se v nich nevyskytují žádné objekty, anebo se v PDS reprezentují jen takové, které objekty obsahují. Rozdělení prostoru P je prováděno na principu rekurzivní dekompozice (podobně jako metody divide at impera), obvykle řezem nadrovinou. Rozlišuje se také, zdali při těchto řezech je ovlivněna pouze jedna kapsa nebo více.
Dalším kriteriem klasifikace je, zdali jsou podprostory disjunktní, nebo zdali se mohou překrývat. Jinou možností může být kritérium rovnoměrnost rozložení dat v prostoru.
PDS lze klasifikovat také podle toho, uvažujeme-li pouze vícerozměrné body nebo prostorové objekty nenulové velikosti. Pro bodové objekty byla v minulosti vyvinuta řada metod. Připomeňme k-d-stromy, vícerozměrnou mřížku (grid file), čtyřstromy (quad-trees) či buddy-stromy. Některé z nich se dají zobecnit pro obecnější prostorové objekty. Obecnější objekty se většinou organizují pomocí R-stromů a jejich četných variant.
2.1 Transformační přístup
V prostředí databází, jejichž data jsou založena na záznamech, je snadné si představit, že záznam je vlastně bodem vícerozměrného prostoru. Např. řádek tabulky
MĚSTO(Název, Počet_ob, Adresa_magistrátu, Rozloha)
je prvkem čtyřrozměrného prostoru. Takové body lze organizovat např. ve vícerozměrné mřížce (viz např. [Po97]), jejíž osy odpovídají sloupcům tabulky a body na osách prvkům domén sloupců. Stačí, aby na doménách bylo definováno uspořádání. Pak problém např. intervalového dotazu na města s rozlohou mezi 12-15 km2 a 10-30 tisící obyvatel znamená najít jistou kostku v prostoru a v ní odpovídající body.
Použijeme-li tuto ideu pro prostorové objekty výchozího prostoru P, můžeme se dostat prostorů dimenzí stejných, nižších, ale i vyšších než dimenze P. Např. úsečku ve 2-rozměrném prostoru lze reprezentovat pomocí souřadnic jejích krajních bodů jako bod (x1, y1, x2, y2) v čtyřrozměrném prostoru. Říká se někdy, že objekt je reprezentován reprezentativním bodem. Obecněji jde o transformace z prostoru dimenze k do prostoru dimenze 2k.
Kromě zvyšování dimenze je další nevýhodou takových transformací, že nezachovávají sousedství, což má v důsledku vliv na efektivnost prostorových operací. Jsou-li 2 linie blízko sebe v 2-rozměrném prostoru, neznamená to, že jsou u sebe blízko 2 odpovídající body čtyřrozměrného prostoru.
Jinou možností je rozdělit prostor na buňky stejné velikosti a očíslovat je v souladu s nějakou vyplňující křivkou (Peanova, Hilbertova – viz např. [Po99]). Prostorový objekt může být reprezentován pomocí množiny čísel nebo dokonce jako jednodimenzionální objekt. Tím se dostáváme k transformaci do prostoru nižší dimenze. Na jednodimenzionální objekty lze potom použít běžný B-strom.
2.2 Použití nepřekrývajících se oblastí
Prostor P je rozdělen do navzájem disjunktních podprostorů. Můžeme se setkat se dvěma typy metod (pozn.: Někdy se nerozlišuje mezi oběma metodami a hovoří se pouze o stříhání objektů)
V prvním případě se indexují podprostory, tj. nachází-li se objekt v s podprostorech, je Id objektu duplikováno s´ . Ve druhém případě se objekt rozdělí na podobjekty tak, že každý z nich je obsažen právě v jednom podprostoru. Mezi známé PDS prvního typu patří R+-stromy [St86] a buňkové stromy [Gü88].
Všimněme si, že pomocí uvedené reprezentace lze objekty indexovat stejným způsobem jako u jednorozměrných dat. Dokonce ani nezáleží na tom, jestli prostorový objekt je bodem nebo vícerozměrným objektem nenulové velikosti. Vše může být obsaženo v jednom souboru. Pro zachování prostorových vztahů je ovšem výhodné zachovat jistou prostorovou hierarchii pomocí stromu. Duplicity jsou jistě nevýhodou, rovněž operace INSERT a DELETE budou vyžadovat větší režii.
Samet v [Sa95] upozorňuje na fakt, že uvedené metody jsou datově závislé, tj. podprostory odpovídají v nějakém smyslu prostorovým objektům, což může komplikovat některé operace. Jinou variantou je, rozdělit prostor rovnoměrně (mřížka) nebo použít čtyřstromy ([Sa84]). První případ se uplatní v prostředí rovnoměrně rozložených objektů (např. domy v městě), ve druhém případě na rozložení dat nezáleží.
Uvažujeme-li jako prostorové objekty pouze body, jsou metody nepřekrývajících se oblastí vhodné. Lze sem zařadit např. klasické k-d-stromy nebo k-d-B-stromy a mnoho dalších.
2.3 Použití pokrývajících oblastí
Základní ideou je, že každý objekt je obsažen právě v jednom z podprostorů P, který tvoří pokrývající oblast objektu. Typicky je pokrývající oblastí minimální ohraničující kostka či ve dvourozměrném případě obdélník (MOO). V článku budeme používat většinou dvourozměrný případ a tedy vystačíme s pojmem MOO. Připomeňme, že MOO není jedinou variantou. Pokrývající oblastí může být libovolný mnohoúhelník, ale i kružnice, či elipsa. Oblasti se odlišují v režii nutné ke své reprezentaci a velikostí tzv. mrtvého prostoru (prostor mezi pokrývaným a pokrývajícím objektem).
Pokrývající oblasti jsou konstruovány hierarchicky (většinou zdola nahoru), mohou se překrývat a jsou obvykle organizovány jako stromová struktura. Nejznámějším představitelem tohoto přístupu je R-strom [Gu84] a jeho četné varianty.
Dosáhnout efektivnosti zpracování takových struktur může být složité. Cílem je minimalizovat překrývání MOO. Získá se tím totiž větší šance na projití méně cest ve stromě při hledání nějakého objektu. Speciálním problémem je pak údržba PDS, protože změny v konfiguraci objektů mohou vyvolat změny MOO.
3. Prostorové datové struktury pro indexaci bodů
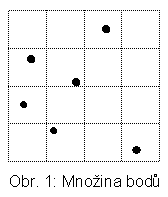
V úvodu se zmíníme o PDS, které slouží pro indexování bodů. Popíšeme stručně čtyřstromy, k-d-stromy a vícerozměrnou mřížku. Ve všech případech se rozděluje celý prostor P, u vícerozměrné mřížky se rozdělují i ty kapsy, které zůstávají prázdné. Pro výchozí situaci budeme předpokládat body na obr. 1. Pro snazší manipulaci jsou umístěny v pravoúhlé pravidelné mřížce.
 |
 |
 |
Z dalších známých PDS této kategorie jmenujme alespoň buddy-stromy ([SK90], též i [Po97]).
3.1 Čtyřstromy
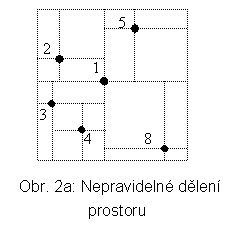
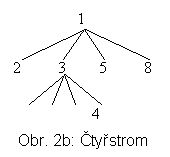
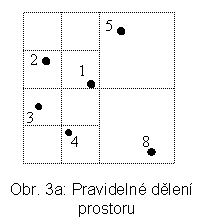
Již bylo zmíněno, že kořeny PDS sahají hluboko do historie informatiky. Idea čtyřstromů pochází z r. 1974 [FB74], kdy Finkel a Bentley navrhli první variantu. PDS čtyřstromy je určena pro dvourozměrný prostor P, který se dělí rekurzivně vždy na 4 podprostory. Ty se značí tradičně SZ, JV, JZ a SV. Obecně nemusí být stejné velikosti (viz obr. 2a a odpovídající čtyřstrom na obr. 2b). V pravidelné dekompozici P (regular quadtrees) obdržíme např. situaci na obr. 3a se čtyřstromem na obr. 3b. V odpovídajícím stromu má každý vnitřní uzel 4 následníky (korespondence větví ke kvadrantům je v obou případech zleva SZ, JV, JZ, SV.
 |
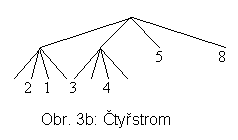 |
Počet bodů v každé buňce (kapse) je v příkladě stanoven na 1, může být však omezen nějakým číslem b. Pro k dimenzí budou mít vnitřní uzly takových stromů 2k následníků.
Shrneme-li, vidíme, že čtyřstromy nejsou vyvážené. Na vyváženost mohou mít vliv nerovnoměrně rozložená data nebo pořadí vkládaných objektů. Lze dost obtížně zobrazit do stránek na vnější paměti. Ve stránkách by ovšem mohl být obsah listů, tj. záznamy reprezentující 1 až b bodů. Číslo b tedy může souviset s blokovacím faktorem stránky.
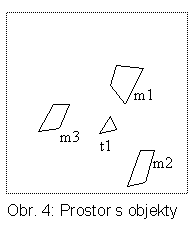
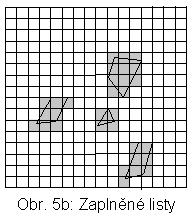
Zobecnění na objekty nenulové velikosti nemusí být složité. Pro situaci na obr. 4 lze prostor dělit např. tak, jak ukazuje obr. 5a. Výsledný čtyřstrom by měl 4 úrovně (obr. 5a), jeho některé listy (šedé na obr. 5b) by obsahovaly (vícenásobně) identifikátor objektů m1, m2, m3 a t1.
 |
 |
 |
Dotazy na obsah oblasti, tj. např. “Najdi všechny objekty uvnitř D”, zřejmě nebudou problémem. Složitější naopak bude dotaz na umístění objektu v prostoru P.
3.2 k-d-stromy
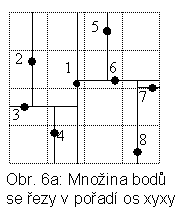
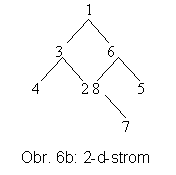
Hezkým příkladem prapředka několika PDS je dobře známý k-d-strom. Jde o k-dimenzionální datovou strukturu formulovanou Bentleyem v již v r. 1975 [Be75]. Strom na obr. 6b reprezentuje řezání prostoru P nadrovinami (zde přímky), přičemž jejich směr alternuje mezi k (zde 2) možnostmi (obr. 6a).
Uzly k-d-stromu obsahují souřadnice bodů a eventuálně tzv. diskriminátor (číslo mezi 0 a k-1), které říká, podle které osy je proveden řez. Nevýhodou k-d-stromu je opět jeho citlivost na pořadí, ve kterém body do struktury vstupují. Strom je samozřejmě výškově nevyvážený.
Z hlediska databází prostorových objektů je zajímavá varianta k-d-B-strom navržený Robinsonem v r. 1981 [Ro81]. Jde o kombinaci k-d-stromu a B-stromu. Zobrazuje totiž k-d-strom do stránek. Prostor P je rozdělen na nepřekrývající se podprostory pomocí řezů podobně jako u k-d-stromu. Body jsou uloženy ve stránkách – listech. Hierarchie dělení podprostorů je reprezentována ve vnitřních uzlech stromu, z nichž každý je také reprezentován stránkou na vnější paměti.
 |
 |
Výsledný strom je vyvážený, trpí však nedostatečným využitím kapacity stránek. V dynamice k-d-B-stromu se štěpí přeplněné stránky obsahující body a toto štěpení se propaguje do rodičovských stránek. Ty se mohou štěpit také (podobně jako u B-stromu). Toto štěpení však muže vyvolat další štěpení směrem k listovým uzlů. Tak vznikají nevyužité podprostory, které jsou v PDS reprezentovány. To snižuje efektivnost zpracování dotazů na oblast (Najdi všechny objekty překrývající se s D) či na obsah oblasti. Řešením jsou další modifikace – např. hB-stromy (děravé – z angl. holey).
Další modifikací k-d-stromů jsou varianty umožňující se odpoutat od pouhých bodů. Prostorové k-d-stromy (skd-stromy) byly vyvinuty v roce 1987 [Oo87].
3.3 Vícerozměrná mřížka
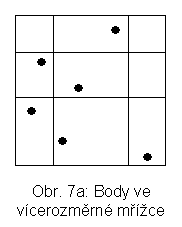
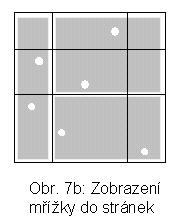
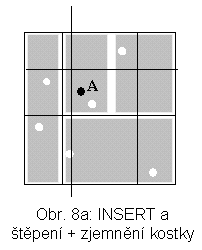
Ve vícerozměrné mřížce je každá osa (zde x, y) rozdělena v nějakém počátečním dělení, které se nazývá škála. Jde o počáteční rozdělení množiny, na které se předpokládá uspořádání, na intervaly. Odpovídající pravoúhlé řezy určují mřížku, skládající se z tzv. základních kostek. Např. vícerozměrná mřížka na obr. 7a má 9 základních kostek. Obsah základních kostek je zobrazen do stránek na vnější paměti tak, že ve stránce může být více kostek. Ty musí tvořit konvexní útvar. Jedno z možných zobrazení pro situaci na obr. 7a je na obr. 7b. Blokovací faktor je 2, tj. jsou nutné 3 stránky. Vložíme-li bod A a je třeba štěpit stránku, lze provést buď zjemnění mřížky (situace na obr. 8a) nebo štěpení proběhne při zachování původní mřížky (obr. 8b). Zjemnění představuje řez mřížky nadrovinou (pro k dimenzí je možné k směrů takových řezů).
 |
 |
Škály a vícerozměrná mřížka jsou uloženy v polích, ze kterých je přímý přístup na stránky na vnější paměti. V implementacích se pole realizují pomocí stromů či hašováním.
 |
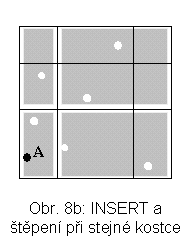 |
Jak již bylo zmíněno v odstavci 2.2, lze vícerozměrnou mřížku použít na libovolná vícerozměrná data, v jejichž každé dimenzi je definováno uspořádání. Velmi efektivně se ve vícerozměrné mřížce budou realizovat dotazy na oblast a obsah oblasti. Její výhodou je také skutečnost, že je sama o sobě koncipována pro data na vnější paměti.
4. Prostorové datové struktury pro indexaci obecných objektů
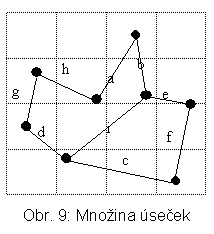
Pro indexaci obecných objektů se zdají perspektivní především PDS pokrývající oblasti. Je zajímavé, že některé PDS pro indexaci bodů jsou modifikací PDS určených hlavně pro obecnější objekty. V článku budeme používat situace na obr. 4 a 9.
4.1 R-stromy a jejich varianty
R-strom, navržený Guttmanem v r. 1984 [Gu84], představuje jednoduchou modifikaci B-stromů, kde záznamy v listových uzlech stromu obsahují ukazatele k datovým objektům reprezentujícím prostorové objekty. Ty mohou být reprezentovány pomocí Id. Podstatné je, že uzel R-stromu je implementován jako jedna stránka na vnější paměti. To ovlivňuje návrh řádu R-stromu (viz dále).
Vlastní indexace objektů je dána pomocí dvojic (I, Id), přičemž I je MOO ohraničující odpovídající prostorový objekt. Tyto dvojice budeme nazývat indexové záznamy. Každé I má obecně tvar (I0, I1,..., Ik-1), kde Ii je interval [ ai,bi] popisující ohraničení objektu v dimenzi i. Pro k = 2 tedy potřebujeme 4 parametry. Vnitřní uzly obsahují záznamy tvaru (I, ukazatel), přičemž ukazatel ukazuje na podstrom v R-stromu takový, že I pokrývá všechny MOO, které se v něm vyskytují. Na rozdíl od B-stromu není striktně dodrženo pravidlo o polovičním naplnění uzlů v nejhorším případě. Je-li R-strom m-ární strom, pak m1 bude označovat parametr, pro který platí m1 £ m/2. Někdy se R-stromy vybavují řádem (m1, m). Minimální počet následníků uzlu R-stromu bude m1. R-strom řádu (m1, m) je tedy m-ární strom, který má následující vlastnosti:
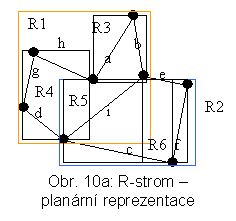
Pro E indexových záznamů je v nejhorším případě hloubka R-stromu [logmE] -1, nejhorší naplněnost stránky je m1/m. Příklad R-stromu pro m1 = 2 a m = 3 pro objekty na obr. 9 je na obr. 10a a 10b. (pozn.: detailnější a rozsáhlejší příklad je uveden v [Po 99]
 |
 |
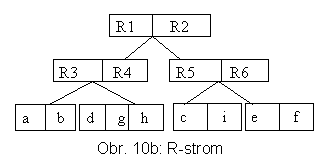 |
R-strom je struktura dynamická, tj. je založena na štěpení stránek (pro operaci INSERT) a slévání stránek (pro operaci DELETE). Na rozdíl od B-stromů není hledání v R-stromu určeno jednou větví. Protože MOO v jednotlivých podstromech se mohou překrývat (na obr. 10a např. R1 a R2 nebo R5 a R6), je možné, že existuje více než jedna možnost, jak pokračovat při prohledávání stromu z jednoho uzlu. Tím je hledání složitější. Veškeré optimalizace používané při konstrukci R-stromu jsou založeny na požadavku, co nejvíce separovat MOO, aby se omezil prostor vyhledávání. Z toho plynou speciální požadavky na algoritmus operace INSERT, ve kterém se realizují různé heuristiky nabízející víceméně uspokojivá řešení daného problému.
Algoritmus vkládání indexového záznamu do R-stromu má tedy pro následné zpracování dotazů zásadní důležitost. Je založen na strategii nalézt takovou větev ve stromě, tj. takový list R-stromu, že opravy kostek po cestě ke kořenu povedou k co nejmenším změnám. Důležitá bude i procedura pro štěpení. Tam se řeší problém, jak rozdělit neuspořádanou množinu kostek do dvou uzlů. Rozdělení záznamů do dvou uzlů je děláno tak, aby bylo co nejméně pravděpodobné, že bude potřeba oba uzly při prohledávání zkoušet. Protože uzly jsou navštěvovány z uzlu-předchůdce, je nutné minimalizovat objem odpovídající oblasti I. Tyto akce se mohou propagovat v nejhorším případě až do kořene R-stromu.
Pro rozdělení obsahu uzlů je možné použít algoritmus uvažující všechny možnosti. Hledá se globální minimum, přičemž algoritmus má exponenciální složitost. Guttman uvádí další algoritmy, lineární a kvadratický, které pouze aproximují řešení.
Při konstrukci R-stromu je třeba také zvažovat dynamiku prostředí aplikace, do které bude umístěn. Je rozdíl, když R-strom vzniká postupnými aplikacemi operace INSERT nebo jsou prostorové objekty předem známy. Ve druhém případě je možné je předzpracovat a pak teprve vytvořit R-strom. Objekty prostorově blízko sebe se seskupují (tzv. pakování) a R-strom vzniká dávkově, zdola nahoru. Pakování se provádí např. v souladu s nějakou vyplňující křivkou (tj. linearizací), existují ale i možnosti provádějící konstrukci R-stromu přímo v k dimenzích. Blíže pojednává o optimalizačních problémech konstrukce R-stromů práce [Ga94].
R-stromy jsou jednou z nejcitovanějších PDS. Slouží často jako referenční PDS pro srovnávání s jinými PDS.
4.2 R*-stromy
Původní R-strom byl založen na heuristické optimalizaci s kriteriem minimalizovat velikost prostoru každého I, který se vyskytuje ve vnitřních uzlech R-stromu. R*-strom [BKSS90] zahrnuje kombinovanou optimalizaci velikosti ohraničujícího prostoru, velikosti okraje I (u MOO je to jeho obvod) a velikosti překrytí těchto prostorů. Za cenu poněkud složitější implementace se docílí provozně efektivnější varianty než poskytuje R-strom.
Smyslem minimalizace velikostí ohraničujícího prostoru je minimalizace mrtvého prostoru. To zlepšuje rozhodování, kterou cestou se vypravit při prohledávání uzlů na vyšších úrovních. Minimalizace překrytí snižuje počet cest, které je nutné při prohledávání struktury projít. Zmenšování povrchu ohraničujících prostorů vede u MOO ke čtvercům.
Zajímavé je, že se stoupajícím počtem dimenzí se výkon R*-stromů prudce snižuje. Výsledky [BKK96] ukazují, že např. 8-rozměrná data se prohledávají 10´ pomaleji, než 3-rozměrná. Důvodem je, že se zvyšuje překrývání ohraničujících podprostorů použitých ve vnitřních uzlech (v daném případě 20´ ).
Současným řešením mohou být např. X-stromy [BKK96], které modifikují R-stromy tak, že minimalizují překrývání v uzlech vyšší úrovně. Pomáhají tzv. superuzly (jistá lineární pole), které uchovávají informace o štěpení. Pomocí X-stromů se výkon R*-stromů zvyšuje až o 2 řády. Teoreticky dobře propracovaný přístup představují VP-stromy [BKK96]. VP-stromy (angl. Vantage-Point tree) [Yi93] jsou založeny na rozdělování prostoru podle relativních vzdáleností mezi body, než podle jejich absolutních souřadnic. Pro dělení podprostorů se místo k osám paralelních nadrovin používají speciální “vyhlídkové body” (vantage points). V jednom ze vniklých podprostorů jsou body bližší, v druhém ty vzdálenější.
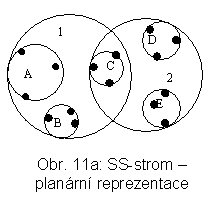
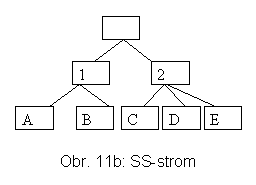
4.3 SS-stromy
SS-stromy (pozn.: Pozor, pojem SS-stromy se používá také pro zcela jinou PDS - tzv. spatial spay trees.) [WJ96] byly navrženy speciálně pro dotazy na nejbližšího souseda v prostorech vysokých dimenzí, kde se PDS jako k-d-B-stromy a R*-stromy uplatňují obtížně. Jedním z jejich základních rysů je, že používají omezující kružnice. Jejich střed je totožný s těžištěm konfigurace, pokrývaných bodů. Při vstupu nového bodu p algoritmus INSERT určuje nejvhodnější podstrom, jehož těžiště je nejblíže p. PDS je samozřejmě struktura dynamická, při přeplnění uzlů dochází ke štěpení. Kružnice je v prostoru dimenze k reprezentována k+1 parametry, na rozdíl od pokrývajících kostek s 2k+1 parametry. Tím se zvětšuje počet záznamů v uzlech a snižuje hloubka stromu.
Příklad SS-stromu poskytují obr. 11a a 11b.
 |
 |
SR-strom [KS97] je rozšířením R*-stromů a SS-stromů. Odlišujícím rysem SR-stromů je, že kombinují ohraničující kružnice a MOO (zde čtverce). To zlepšuje, ve srovnání s R*-stromy a SS-stromy složitost dotazu na nejbližší sousedy redukcí jak velikosti objemu oblastí tak jejich průměru. SR-stromy také překonávají své předchůdce v situacích, kdy data nejsou rovnoměrně rozložená.
4.4 R+-stromy
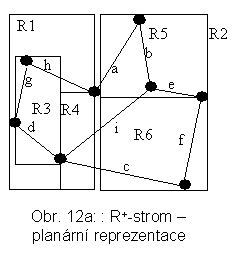
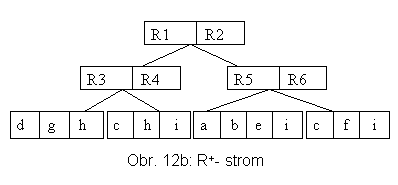
R+-stromy mohou být chápány jako rozšíření k-d-B-stromů pro práci s prostorovými objekty, které mají nenulovou velikost. Na rozdíl od k-d-B-stromů není rozdělen celý prostor P, nýbrž jen to, co je nutné. Jsou použity MOO, které se ale nepřekrývají. Důsledkem tohoto přístupu ovšem je, že dochází ke stříhání objektů. Je také upuštěno od požadavku, aby počet záznamů v uzlu neklesl pod m1.
Na rozdíl od R-stromů, při může být operaci INSERT objekt přidán do více listů (jeho odpovídající MOO se dekomponuje). Štěpení uzlů může, podobně jako u k-d-B-stromů, vést nejen k propagaci změn do rodičovských uzlů, ale následně i jejich dalších, synovských.
Obr. 12a a 12b naznačují možnost řešení pro situaci na obr. 9.
Testy autorů metody ukázaly, že v případě dotazů na body se ušetřilo 50% přístupů na vnější paměti (disk). Dotazy totiž vyžadují průchod stromem pouze po jedné cestě. Pro dotazy, kdy prostorový objekt překrývá MOO, je samozřejmě nutné do více větví vstoupit.
 |
 |
4.5 Semínkové stromy
Uvažujme na chvíli dotaz D1. Jak pro obrysy měst, tak pro silnice může existovat zvláštní indexová struktura daná R-stromem.Vyhodnocení dotazu pak vede jistému prostorovému spojení těchto struktur (prostorových relací), kde operace spojení dvou objektů je založena na průniku prostorových objektů. Požadavek na spojení ovšem může vzniknout i tehdy, kdy je spojení součástí složitějšího dotazu a to, co se spojuje, vniklo dynamicky předchozím zpracováním. Budovat index pomocí obyčejného R-stromu je pak časově neúnosné. Řešením mohou být semínkové stromy [LR98]. Jejich hlavní předností je, že umožňují rychlé vybudování datové struktury, tj. používají speciální algoritmus operace BUILD.
Semínkové stromy jsou vlastně R-stromy, které mají úrovně rozdělené do dvou kategorií – semínkové a růstové. Směrem od kořene je několik úrovní semínkových, zbyle jsou růstové. R-strom se pak ukládá tak, že R-stromy zakořeněné z poslední semínkové úrovni jsou ukládány zvlášť (tvoří les R-stromů). Semínková úroveň může být společná pro více množin objektů (prostorových relací), generují se pouze růstové úrovně. Efekt takto rozdělené struktury je enormní. V práci [Be99] se pro prostorové spojení dosahuje semínkovými stromy režie pouze několik procent z původního času potřebného pro vytvoření R-stromu.
4.6 Buňkové stromy
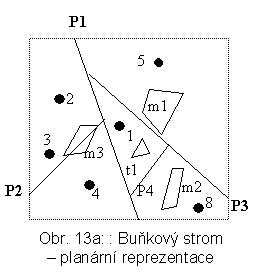
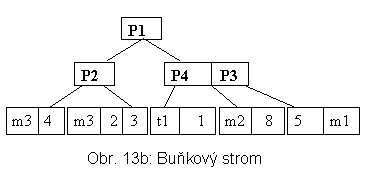
Mezi PDS, které dělí prostor na disjunktní části se řadí buňkové stromy [Gü88]. Na rozdíl od R+-stromů se dekomponuje celý prostor P a navíc ještě nadrovinami do konvexních mnohoúhelníků. Umožňuje to tak indexovat lépe prostředí prostorových objektů, které mají obecnější konvexní tvary než obdélníky. Samozřejmě dochází ke stříhaní objektů. Chceme-li umístit do P nekonvexní objekt, je nutné ho střiháním také dekomponovat (ne nutně disjunktně). Výsledkem tedy může být, že jedna komponenta může zasahovat do více podprostorů. Je tedy rozdělena do buněk, které jsou umístěny v listech.
Dělení podprostorů je binární, tj. lze je popsat binárním stromem (BS). Zamezí se tím komplikacím se stříháním objektů. Výsledná struktura může být tedy chápána jako zobrazení prostoru rozděleného pomocí BS do stránek, nebo jako kombinaci BS a R+-stromu. Příklad buňkového stromu je na obr. 13a a 13b.
 |
 |
5. Závěr
Existence množství PDS různých provozních vlastností vede k myšlence, že je velmi nutné pečlivě zvážit, jakou strukturu pro danou aplikaci použít. Výběr je problémem, protože existuje mnoho kritérii optimality, mnoho parametrů, které ji ovlivňují. Hodně též závisí na prostorových objektech. PDS může být vhodná pro jednu sadu objektů a nevhodná pro jinou. Optimalizace pro bodové objekty se může ukázat nevhodná pro zpracování oblastí. Problematické je i použití testovacích množin objektů. Závisí mnohdy i na programátorských tricích, technice vyrovnávacích pamětí apod.
Protože zatím neexistuje jedna robustní struktura umožňující implementovat jakýkoliv prostor spojený s libovolnou aplikací prostorových objektů, je otázkou, jak by měl vypadat odpovídající univerzální software. V každém případě by měl nabídnout více PDS. Jinou možností je mít software specializovanější, vytvořený pro jisté třídy aplikací.
Vedle některých komerčních producentů GIS, které zahrnují do svých produktů databáze, je zajímavé sledovat vývoj a nabídku prostorových databází jako takových. Např. Informix vyvinul technologii datablade založenou na speciálních účelově orientovaných “zasouvacích” modulech, které rozšiřují možnosti základního relačního databázového stroje. Nabízí vedle modulu MapInfo Geocoding také tzv. Spatial datablade, který je založen na R-stromech. Cílem je vyvíjet a nabízet takové moduly ve vícenásobných implementacích (zřejmě s použitím různých PDS) se zachováních stejné funkcionaliaty. Tedy uživatel si bude moci vybrat v závislosti na požadavcích svých aplikací.
Zdá se, že podobnou cestou vykročily i další databázové firmy produkující tzv. univerzální servery. Např. univerzální server ORACLE využívá speciální typ dat HHCODE založený na technologii čtyřstromů. Firma ESRI (http://www.esri.com) nabízí několik produktů pro prostorové databáze aplikované v systému ARC/INFO. Její Spatial Database Engine (SDE) pracuje s prostorovými daty uloženými v ORACLE, Informix, Sybase a v dalších databázích.
Jiným problémem je, jak jsou PDS odolné vůči datům, která vykazují nějaké nerovnoměrnosti. Může jít jednak o nerovnoměrné rozložení prostorových objektů v prostoru, nebo o značné rozdíly mezi rozměry prostorových objektů. Teorie již dnes zná postupy, jak řešit tyto problémy, např. úpravou původních algoritmů, které se samy rozhodnou, jakou strategii zvolit v případě zjištění vlastností prostorových dat.
Oblast výzkumu PDS zdaleka není uzavřena. Zjišťuje se např., že techniky používané v 2D nebo 3D, jako R- či R*-stromy nemusí být výhodné v prostorech vysokých dimenzí.
Nové požadavky na prostorová data jsou formulovány i v dalších aplikacích. Vícedimenzionální data používající nějaké (prostorové) metriky se vyskytují i v takových oblastech jako molekulární biologie, zpracování řetězců, zpracování barevných histogramů atd. Vznikají tedy další PDS – např. X-stromy, varianty VP-stromů a další.
Mezi další inspirativní zdroje problémů patří techniky prostorového spojení, paralelizace operací, dotazy na nejbližší sousedy, analýza algoritmů prostorových operací PDS, pakovací algoritmy, chování PDS v prostorech vysokých dimenzí.
Poděkování
Dík patří Dr. Ing. Jiřímu Horákovi, jehož podnětné připomínky přispěly k vytvoření finální verze článku.
Literatura
[ Be75] Bentley, J.: Multidimensional Binary Search Trees used for Associative Searching. Communications of ACM, 18, 9, Sep. 1975, pp. 509-517.
[ Be97] Bertino, E. et al: Indexing techniques for advanced database systems. Kluwer Academic Publ., 1997.
[Be99] Beneš, R.: Vícerozměrné datové struktury a jejich použití v GIS. Diplomová práce MFF UK, 1999.
[ BKK96] Berchtold, S., Keim, D.A., Kriegel, H.-P.: The X-tree: An Indexed Structure for High-Dimensional Data. Proc. 22th Int. Conf. on VLDB, Bombay, India, 1996.
[ BKSS90] Beckmann, N. et all: The R* -tree: An Efficient and Robust Access Method for points and Rectangles. Proc. 1990 ACM/SIGMOD International Conf. on Management of Data, May, Atlantic City, USA, 1995, pp. 23-25
[ FB74] Finkel, R., Bentley, J.: Quad Trees: A Data Structure for Retrieval on Multiple Keys. Acta Informatica, Vol. 4, No. 1, 1974, pp. 1-9.
[Ga94] Gavrila, D.M.: R-tree Index Optimization. CAR-TR-718, Comp. Vision Laboratory Center for Automation Research, University of Maryland, 1994.
[ GG98] Gaede, V., Günter, O.: Multidimensional Access Methods. Computing Surveys, Vol. 30, No. 2, 1998.
[ Gu84] Guttman, A.: R-trees: a dynamic index structure for spatial searching. Proc. of SIGMOD Int. Conf. of Management of Data, 1984, pp. 47-54.
[Gü88] Günther, D.: Efficient Structures for Geometric Data Management. LCNS No. 337, Springer Verlag, 1988.
[KS97] Katayama N., Satoh S., The SR-tree: An Index Structure for High-Dimensional Nearest Neighbor Queries,'' Proc. of the 1997 ACM SIGMOD Int. Conf. on Management of Data (May 1997) pp. 369-380.
[LR98] Lo, Ming-Ling, Ravishankar, Ch.V.: The Design and Implementation of Seeded Trees: An Efficient Method for Spatial Joins, IEEE Transactions on Knowledge and Data Engineering, Vol. 10, No. 1, January/February 1998.
[Oo87] Ooi, B.C., McDonell, K.J., and Sacs-Davis, R.: Spatial kd-tree: An indexing mechanism for spatial databases. Proc. 11th Int. Conf. on Computer Software and Application,
[OS83] Oshawa, Y., Sakauchi, M.: BD-tree: A new N-dimensional data structure with efficient dynamic characteristics. Proc. 9th World Computer Congress. IFIP, 1983, pp. 539-544.
[Po97] Pokorný, J.: Základy implementace souborů a databází. Skripta MFF UK, Vydavatelství Karolinum, Praha, 1997.
[Po99] Pokorný, J.: Prostorové datové struktury. Sborník konference GIS’98, Ostrava, 1998.
[Ro81] Robinson, J.T.: The k-d-B-tree: A search structure for large multidimensional dynamic indexes. Proc. 1981 ACM SIGMOD Int. Conf. on Management of Data, 1981, pp. 10-18.
[Sa84] Samet, H: The quadtree and related hierarchical data structures. ACM Computing Surveys 16, 2, 1984, pp. 187-260.
[ Sa90a] Samet, H: Applications of Spatial Data Structures: ComputerGraphics, Image Processing and GIS. Addison Wesley, Reading, MA, 1990.
[ Sa90b] Samet, H: The Design and Anylysis of Spatial Data Structures. Addison Wesley, Reading, MA, 1990.
[ Sa95] Samet, H: Spatial Data Structures. In: Modern Database Systems: The Object Model, Interoperability, and Beyond (W. Kim, ed.), Addison Wesley/ACM Press, Reading, MA, 1995.
[ SK90] Seeger, B., Kriegel, H.-P.: The Buddy-Tree: An Efficient and Robust Access Method for Spatial Data Base Systems. Proc. of the 16th VLDB Conference, Brisbane, Australia, 1990.
[St86] Stonebraker, M. et al: An Analysis of rule indexing implementation in database systems. Proc. of 1st Conf. on Expert Data Base Systems, 1986.
[Su98] Subrahmanian, V.S.: Principles of Multimedia Database Systems. Morgan Kaufmann Publishers, Inc., San Francisco, CA, 1998.
[Yi93] Yianilos, P.N.: Data Structures and Algorithms for Nearest Neighbor Search in General Metric Spaces , Proceedings of the Fourth ACM-SIAM Symposium on Discrete Algorithms, January 1993.
[WJ96] White, D. A., Jain, R.: Similarity Indexing with the SS-tree. Proc. of 12th Int. Conf. on Data Engineering, New Orleans, USA, 1996, pp. 516-523.