Zpracování dat v prostředí GIS s využitím teorie Rough set

Jaroslav Smutný
Ústav železničních konstrukcí a staveb
VUT FAST
Veveří 95
662 37 Brno
Tel.: +420 5 4117325 Fax: +420 5 745147
E-mail: zksmu@fce.vutbr.cz

Rough set theory, introduced by Professor Zdzislaw Pawlak in the early1980s, is a relatively new mathematical tool to processing date with vagueness and uncertainty. This approach seems to be of fundamental importance in problems of artificial intelligence and cognitive sciences, in the areas of machine learning, knowledge acquisition, decision analysis, expert systems, but this date can be utilised upon implementation of analysis in areas geographical information systems.

Teorie Rough set, vytvořená profesorem Zdzislawem Pawlakem počátkem osmdesátých let, představuje poměrně nový matematický nástroj pro práci s daty, které jsou charakterizovány neurčitostí a nejistotou. Taková data nabývají základního významu při zpracování problematiky umělé inteligence a rozpoznávání, dále v oblasti strojového učení, znalostního inženýrství, rozhodovací analýze, expertních systémů, ale mohou být použita při provádění analýz v oblasti geografických informačních systémů.

V posledních cca 20 let se objevila a objevuje řada metod a idejí (jazykové modely na bázi fuzzy matematiky, Rough množin, teorie chaosu, neuronových sítí apod.), které vznikaly na základě tlaku praxe na potřeby studia a modelování složitých a vágně definovaných systémů. Úspěch těchto modelů spočívá především v tom, že se s pojmem vágnosti vyrovnaly na úrovni interpretace nových matematických teorií a nikoliv užitím “vágního formálního aparátu”. Při jejich praktických aplikacích se však naráží na řadu konkrétních problémů plynoucích ze skutečnosti, že jsou velmi malé zkušenosti s formulací konkrétních reálných úloh pomocí těchto nových formálních nástrojů, případně neexistuje metodologie tohoto druhu modelování a často neexistuje ani potřebné programové vybavení. Ne jinak je tomu i v problematice zadávání a řešení profesně různých úloh s využitím geografických dat a objektů. I pro tuto oblast je tedy nutné formulovat nové úlohy vycházející z existence geografických objektů, aplikovat nové matematické teorie a vytvářet nové aplikační programové vybavení.

Teorie Rough množin reprezentuje jeden z prvním nestatistických přístupů k analýze dat. Je založena na předpokladu, že v daném prostoru ke každému objektu, který zkoumáme, jsou přiřazeny určité informace (data, vlastnosti). Například objekty mohou být určité geografické entity, kterými se při řešení daného problému zabýváme (parcely, domy, plochy, ale i liniové stavby apod.). Informace jsou tvořeny textovými údaji přiřazenými těmto objektům. Objekty se stejnými informacemi (vlastnostmi) jsou nerozlišitelné (podobné nebo stejné) z pohledu dostupných informací o těchto objektech. Takto chápaný popis nerozlišitelnosti představuje filozofický základ teorie Rough množin. Jakákoliv skupina nerozlišitelných objektů je nazývána elementární množinou. Libovolná podmnožina daného prostoru může být vyjádřena přesně nebo přibližně.

V prvním případě daná podmnožina může být charakterizována dvěma seskupeními nazývanými spodní a horní aproximace.Tyto dvě aproximace definují Rough množinu. Rozdíl mezi spodní a horní aproximací se nazývá okrajová oblast (region) a zahrnuje objekty, které nemohou být řádně klasifikovány jako patřící nebo nepatřící do příslušné množiny s využitím stávajících znalostí.

Z důvodu snadné algoritmizace je vhodné znalostní databázi (seznam objektů a vlastností) převést do tvaru informační tabulky (viz tab. 1).

Objekty/atributy

a1

  

aj

  

am

x1

a1(x1)

        
           

xi

    

aj(xi)

    
           

xa

        

am(xa)

Tab. 1 Informační tabulka

Řádky této tabulky představují jednotlivé objekty a sloupce představují jednotlivé vlastnosti. Každý řádek v tabulce reprezentuje informace o daném objektu. Formálně můžeme informační tabulku matematicky popsat rovnicí (1).

, (1)

kde S je informační systém, U je konečná množina objektů, Q je konečný počet atributů (vlastností), , přičemž Vq je obor atributu q. Parametr f () představuje tzv. informační funkci. Jakýkoliv pár (q, r); qÎ Q, rÎ Vq pro každé qÎ Q, xÎ U se nazývá deskriptor. V návaznosti na předchozí text lze konstatovat, že záznam v sloupci q a řádku x má hodnotu f(x, q). Objekty x, y Î U jsou stejné (nerozeznatelné) v množině atributů P, jestliže f(x, q)=f(y, q) pro všechny atributy q Î P. Tato skutečnost bývá často označena symbolickým popisem (x, y) Î IND(P). Nechť P Í Q a Y Í U. Spodní aproximaci Y označme PY a horní aproximaci Y označme. Obě dvě aproximace jsou definovány rovnicemi 2 a 3.

(2)

(3)

Množina se často nazývá okrajová oblast (region) (viz. obr. 1). Informační tabulka může být chápána v mnoha aplikacích také jako rozhodovací tabulka za předpokladu, že
Q = C È U a C Ç D = 0. Přičemž množina C představuje atributy vlastností a D rozhodnutí. Rovnice 1 pak přechází na tvar

. (4)

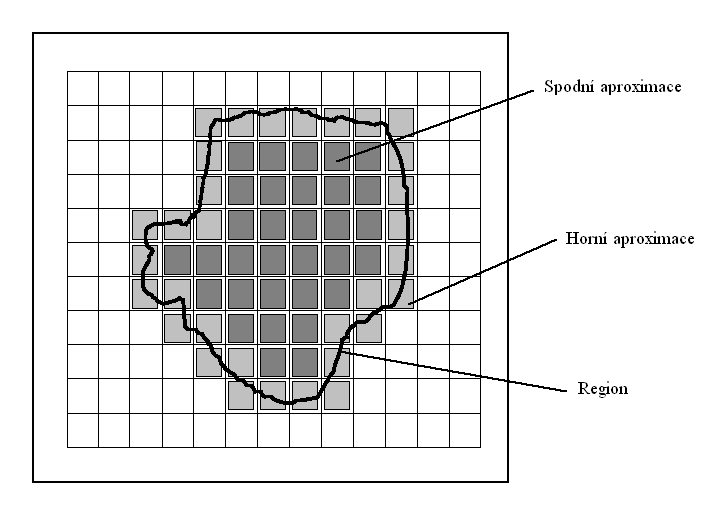
Obr. 1 Grafické zobrazení spodní, horní aproximace a regionu

Algoritmus pro práci s Rough množinami byl nejdříve programován a odzkoušen v prostředí systému Matlab. Tento programový systém se při výběru vhodného vývojového nástroje k sestavení a odladění algoritmu Rough set ukázal jako nejvhodnější. Je to zejména proto, že součástí tohoto matematicky orientovaného programu, jsou dobře využitelné aplikační knihovny pro práci s daty nejrůznějšího typu i původu. K oboustrannému přenosu dat mezi programem Matlab a Geomedia 2.0 bylo použito rozhraní ODBC a sharewarové knihovny Matlab Query.

Po odzkoušení algoritmu a následném seznámení se s programovým rozhraním systému Geomedia, bude algoritmus Rough set postupně implementován formou programové nadstavby do tohoto programu studenty doktorandského studia. Dále bude prezentován velmi jednoduchý příklad. Deset objektů je popsáno čtyřmi vlastnostmi a rozděleno na základě rozhodovacího procesu do dvou základních tříd. V posledním sloupci d = A značí akceptování, d = N nikoliv.

(5)

(6)

(7)

(8)

(9)

(10)

Přesnost aproximace je rovna a . Z rozhodovací tabulky lze následně vygenerovat rozhodovací kritéria. Při shodnosti vlastností hodnocených objektů je možné danou rozhodovací tabulku minimalizovat. V mnoha případech často pracujeme s objekty, které nejsou popsány ve svých vlastnostech kompletně (některé vlastnosti určitých objektů tedy neznáme). Tato skutečnost zvýrazňuje další výhodu teorie Rough množin. Objekty s chybějícími vlastnostmi mohou být buď vyřazeny nebo tyto chybějící vlastnosti mohou být doplněny od objektů s větším počtem známých vlastností.

Objekty

Vlastnosti

Rozhodnutí

a1

a2

a3

a4

d

x1

1

2

1

3

A

x2

1

1

1

1

N

x3

2

1

1

2

N

x4

3

3

1

1

A

x5

3

2

1

1

N

x6

3

3

1

3

A

x7

1

3

0

2

A

x8

2

1

0

3

N

x9

1

1

1

1

N

x10

3

2

1

1

A

Tab. 2 Rozhodovací tabulka - příklad

Přestože teorie Rough množin vzešla z ryze matematického prostředí, nachází už dnes uplatnění v nejrůznějších sférách vědy, výzkumu a praxe. V současné době k nejdůležitějším aplikačním oblastem patří zejména lékařská diagnostika, finanční analýza dat, bankovnictví, rozpoznávání obrazců, písma a řeči.

Přesto se lze oprávněně domnívat, že i v oblasti zpracování dat a realizaci analýz nad platformou geografických informačních systémů, najde tato teorie své uplatnění, zejména pak v oblasti průzkumu a prognózy trhu, dále pak v problematice predikce investiční politiky, vyhodnocování strategie veřejného zájmu, v oblasti demografické analýzy, hodnocení změny a využitelnosti potencionálů, vyhodnocování funkcí území, případně jiných oblastech.

 

Altman E. I: Corporate Financial Distress, J. Wiley and sons, New York, 1983

Brown F. M.: Boolean Reasoning - the Logic of Boolean Equations, 1990, Kluwer Academic Publishers, ISBN 0-7923-9121-7

Pawlak Z., Grzymala-Busse J., Slowinski R., Ziarko W.: "Rough sets." Communications of the ACM, vol. 38, no. 11, 1995

Slowinski R.: Rough set approach to decision analysis. AI Expert, March 1995

Ziarko W.: Review of basics of rough sets in the context of data mining, Proceedings of the Fourth International Workshop on Rough Sets, Fuzzy Sets and Machine Discovery, Tokyo Nov. 6-8 1996

Slowinski R., Zopounidis C., Dimitras A. I.: Prediction of Company Acquisition in Greece by Means of the Rough set Approach, European Journal of operational Research, pp. 2-10, 1997

Slowinski R., Zopounidis C.: Application of the Rough Set Approach to evaluation of Bankruptcy Risk, International Journal of Intelligent Systems in Accounting, Finance and Management 4, 1997