Modelování hierarchické struktury odpovědi s využitím konceptuálních svazů

Daniela Ďuráková, Václav Snášel
Katedra informatiky, FEI
VŠB - Technická univerzita Ostrava
tř. 17. listopadu
708 33 Ostrava - Poruba
E - mail: daniela.durakova@vsb.cz, vaclav.snasel@vsb.cz

Abstrakt

V příspěvku je předvedena možnost hierarchického uspořádání objektů, které byly vybrány v odpovědi na prostorový dotaz s několika parametry. Odpověď na dotaz je ve většině případů tvořena sadou objektů se sledovanými vlastnostmi. Sadu je možné chápat jako kontext a ten pak pomocí teorie konceptuálních svazů hierarchicky uspořádat. V příspěvku je vysvětlen pojem kontext, konceptuální svaz a na příkladu je ukázáno využití této teorie v prostředí geografických informačních systémů.

Abstract

Information systems have a gigantic amount of data stored inside. For the users, mainly in manager positions, it is not sufficient to select data complying with the given demands only, but they expect that selected information will be helpful for them in decisions of everyday work. In this contribution a method is proposed to facilitate hierarchical order of results of query in GIS. For this hierarchical order a theory of concept lattices is applied.

Úvod

Informační systémy v sobě mají uloženo obrovské množství dat. Trh se softwarem nabízí různé způsoby, jak s údaji uloženými v digitální podobě pracovat. Uživatelům, hlavně na manažerských postech, již nestačí pouze vybrat data vyhovující zadaným požadavkům, ale očekávají, že vybrané informace jim pomohou při rozhodování v každodenní práci.

Vyhledávání probíhá nad různými databázemi. Ty mohou obsahovat pouze omezené množství uživatelských dat nebo to naopak mohou být veřejně přístupné databáze velkého rozsahu. V obou případech nastává situace, kdy výsledkem dotazu je množina vyhovujících údajů. Uživatel se pak buď spokojí s výsledkem svého výběru ve tvaru sady více objektů s požadovanými vlastnostmi, nebo vyžaduje možnost dalšího zpřesnění výběru tak, aby bylo nalézt objekt, který zadaným kritériím vyhovuje nejlépe.

V oblasti geografických informačních systémů (GIS) je patrný dvojí přístup k výše uvedenému problému. Na trhu jsou systémy, které pro podporu rozhodování mají implementovány funkce umožňující přiřadit určitou hodnotu požadavkům výběru, jiné se touto problematikou nezabývají. Do první skupiny patří nabídka funkcí Decision Strategy Analysis a Uncertainty Management systému Idrisi z Clark Labs viz [4]. Opačný přístup zvolila vývojová skupina GE Smallworld [6], kdy je ponecháno na uživateli, zda v systému uplatní podobné funkce. Vzhledem k objektovému přístupu je možné rozšířit tento systém o vlastní funkce napomáhající zpřesnění výběru.

Cílem tohoto příspěvku není podrobný popis celé problematiky, ale spíše motivační seznámení s danou problematikou.V příspěvku je popsán postup umožňující hierarchické uspořádání výsledků dotazu v GIS. Příspěvek je pokračování práce [12]. K tomuto hierarchickému uspořádání je použita teorie konceptuálních svazů. Na příkladu výběru lyžařského střediska je předveden způsob využití vytvořeného konceptu k hierarchickému uspořádání výsledků dotazu z prostředí geografických informačních systémů. Jiný přístup použití konceptuálních svazů při vyhledávání je prezentován v [1, 5].

Kontext a koncept

Myšlenka formalizovat pojmy kontext a koncept pomocí teorie svazů není zcela nová. Již dříve existovaly izolované pokusy o využití takzvaných Galoisových svazů a to obzvláště v oblasti Information retrieval, ale teprve práce R. Willeho a jeho skupiny [10, 11] daly vzniknou soustavně budované teorii.

Pro formalizaci pojmu koncept a kontext je použita teorie uspořádaných množin a teorie svazů. Pojmy z těchto klasických disciplin najde čtenář v [2, 3, 9].

Definice 1.Formálním kontextem K  rozumíme trojici (G, M, I), kde G a M jsou množiny a I je relace mezi G a M, to znamená, že I G x M. Prvky množiny G se nazývají objekty a prvky množiny M se nazývají atributy.

Je-li objekt g G v relaci I s atributem m M píšeme gIm nebo (g, m) I. Tento zápis čteme jako objekt g má atribut m. Relace I se nazývá incidenční relace kontextu.

Kontexty menšího rozsahu se jednoduše reprezentují tabulkou. Uvedeme si jednoduchý přiklad kontextu zadaného následující tabulkou. Prvky množiny G je několik živočichů a prvky z množiny M jsou zastoupeny sledovanými vlastnostmi.

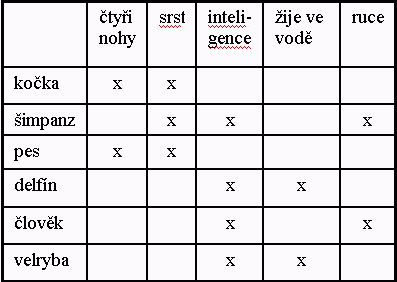
Tabulka 1. Příklad kontextu.

Definice 2. Pro každou množinu objektů A G definujeme A' = {m M gI m g A} , to znamená množinu atributů společných pro všechny objekty z A. Obdobně pro každou množinu atributů B M definujeme B' = {g G gI m m B} , to znamená množinu objektů, které mají všechny atributy z B.

Tvrzení 1. Je-li (G, M, I) kontext, A₁ , A₂ , A₃ G jsou množiny objektů, B₁ , B₂ , B₃ M jsou množiny atributů, potom platí následující vztahy:

1. A₁ A₂ A₂' A₁'

2. A A ''

3. A' = A'''

4. B₁ B₂ B₂' B₁'

5. B B''

6. B' = B'''

7. A B' B A' A x B I

Důkaz tvrzení najde čtenář v [3].

B'' označujeme množinu (B')', to znamená dvojnásobnou aplikaci operátoru z předcházející definice. Splňuje-li dvojice operátorů vlastnosti uvedené v tomto tvrzení hovoříme také o tom, že tyto operátory tvoří Galoisovu konexi (neboli Galoisovu korespondenci) viz [2]. Odtud pochází název Galoisovy svazy.

Definice 3. Formální koncept kontextu (G, M, I) je dvojice (A, B), kde A G, B G, A' = B a B' = A. Množinu A nazýváme extent a množinu B intent konceptu (A, B). Množinu všech konceptů označíme K(G, M, I).

Definice 4. Jsou-li (A₁, B₁), (A₂, B₂) koncepty, potom (A₁, B₁) se nazývá podkonceptem konceptu (A₂, B₂), jestliže A₁ A₂ (to je ekvivalentní s B₂ B₁). Je-li (A₁, B₁) podkoncept konceptu (A₂, B₂) píšeme (A₁, B₁) (A₂, B₂). Je-li (A₁, B₁) podkoncept konceptu (A₂, B₂) říkáme také, že (A₂, B₂) je nadkoncept konceptu (A₁, B₁).

Relace je relace uspořádání na množině všech konceptů K(G, M, I). Tato relace je svazovým uspořádáním na této množině, to znamená že existuje supremum a infimum vzhledem k pro každé dva prvky z K(G, M, I). Důkaz a další podrobnosti najde čtenář v [3]. Relace na konceptech zavádí hierarchickou strukturu, která vzhledem k tomu, že splňuje požadavky na svazové uspořádání, má velmi mnoho vlastností popsatelných matematickým aparátem.

Dále uvedeme základní větu o konceptuálních svazech. Věta obsahuje dvě tvrzení:

• konceptuální svaz je úplný (to znamená, že existuje infimum a supremum pro libovolné podmnožiny nosiče tohoto svazu),
• uvádí předpis pro výpočet suprema a infima.

Supremum budeme označovat symbolem a infimum symbolem .

Základní věta o konceptuálních svazech. Svaz K(G, M, I) je úplný. Infimum a supremum je definováno následujícím předpisem:

kde T je množina indexů, průnik a sjednocení podmnožin přes index t.

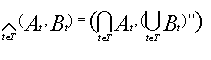
Důkaz této věty najde čtenář v [3].

Na základě vlastností svazů a základní věty o konceptuálních svazech je možné sestavit algoritmus pro nalezení a uspořádání všech konceptů k danému kontextu. V našem případě jsme použili algoritmus popsaný v [8, 9]. Hierarchické uspořádání konceptů je patrné nakreslením Hasseových diagramů daného svazu (viz obrázek 1).

Ukážeme si aplikaci základní věty o konceptuálních svazech při nalezení nadkonceptu c₅ .

({šimpanz}, {srst, inteligence, ruce }) ({delfín, velryba}, {inteligence, žije ve vodě}) = =({šimpanz, delfín, velryba}'', {inteligence}) =

= ({inteligence}', {inteligence}) =

= ({šimpanz, delfín, člověk, velryba}, {inteligence})

Tento výsledek odpovídá vztahu c₁ c₂ = c₅ v konceptuálním svazu na obrázku 1. V tabulce 2 jsou ukázány koncepty pro kontext z příkladu 1 a na obrázku 1 je vykreslen konceptuální svaz pro příklad 1.

Tabulka 2. Koncepty příkladu 1.

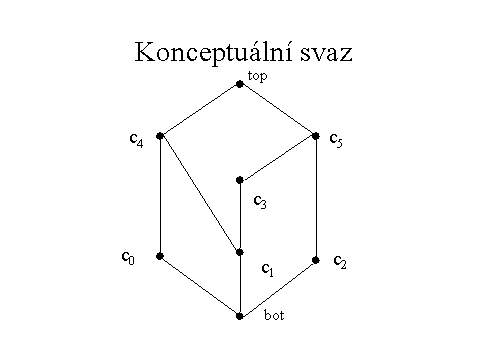
Obrázek 1. Konceptuální svaz příkladu 1.

Uspořádání výsledku prostorového dotazu

Využití předešlé teorie si ukážeme na příkladu vyhledání ideálního místa naší zimní dovolené. Předpokládejme, že jsme zanícení lyžaři a chceme nalézt vhodnou lokalitu v Rakousku pro sjezdové lyžování s možností každodenní relaxace v bazénu. Abychom měli zajištěno, že ve středisku bude sněhová pokrývka, vyžadujeme nadmořskou výšku sjezdovek od 1500m výše.

Nechceme na cestě strávit příliš mnoho času, takže naše požadavky bychom mohli formulovat v následujících bodech:

1. Lokalita vzdálená maximálně 500 km od Prahy.

2. Sjezdovky umístěné minimálně ve výšce 1500 metrů nad mořem.

3. Skipas na více než 20 vleků.

4. Možnost plavání po návratu z lyžování.

Hledání bude prováděno následovně:

1. Nejprve se v mapě zobrazí střediska vzdálená od Prahy maximálně 500 km.

2. Z nich se vyberou taková, jejichž nadmořská výška je alespoň 1500 metrů.

3. Z textových atributů pak u jednotlivých středisek zjistíme uváděný počet vleků.

4. Obdobně zjistíme, zda v místě je možnost návštěvy bazénu či nikoliv.

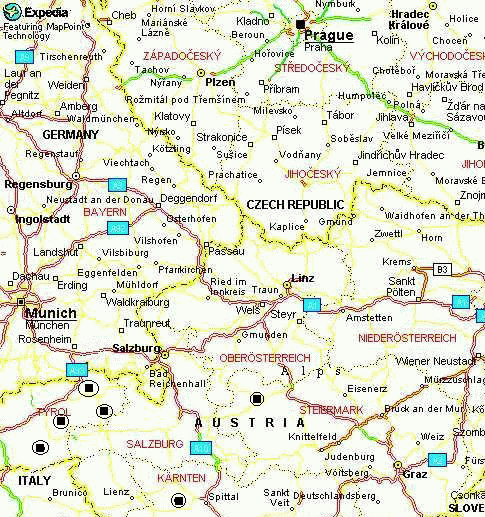
Obrázek 2. Mapa s označenými středisky - výsledek dotazu.

Hledaná střediska jsou vyznačena v uvedené mapě. Výsledek dotazu je zobrazen v tabulce 3, kde jsou uvedeny číselné hodnoty vzdálenosti od Prahy v kilometrech a nadmořské výšky v metrech. V případě skipasu a bazénu jsou hodnoty uvedeny jako boolean - daný atribut středisko má nebo nemá (je nebo není možné na skipas lyžovat na požadovaném počtu vleků, je nebo není možné navštívit bazén přímo ve středisku, případně tyto informace nejsou v propagačních materiálech uvedeny a v odpovědi jim není možné přiřadit pravdivostní hodnotu).

Tabulka 3. Výsledek dotazu

V dalším postupu převedeme vlastnost vyjádřenou numerickou hodnotou na příslušnost do vymezených intervalů. Tento převod vychází z postupu uvedeného v knize Gantera a Willeho [9].

Převod prostorové složky Vzdálenost do tří intervalů je volen z hlediska časové a finanční náročnosti dojezdu do střediska. Kritérium ve formě slovního ohodnocení je použito pro další souvislost s navigací v odpovědi.

Tabulka 4. Převedení numerické hodnoty Vzdálenost

Pro nadmořskou výšku je použito opět převedení do tří intervalů. Dá se předpokládat, že délka trvání a síla sněhové pokrývky bude narůstat s nadmořskou výškou.

Tabulka 5. Převod vlastnosti Nadmořská výška

Převedeme-li číselné hodnoty podle tabulky 4 a 5, můžeme výsledek našeho dotazu zapsat ve formě kontextu, jak je patrné v tabulce 6. Tato kontextová tabulka je výchozí pro vytvoření konceptuálního svazu výsledků dotazu s uvedenými požadavky.

Tabulka 6. Upravený výsledek prostorového dotazu

Použitím algoritmu popsaného Sneltingem [7, 8] nalezneme množinu všech konceptů k tabulce 6. Jednotlivá střediska jsou označena pouze počátečními písmeny svého názvu, vlastnosti středisek výše zavedenými zkratkami.

Z Hasseova diagramu konceptuálního svazu je patrné, že uspořádání konceptů umožňuje výběr středisek s kladením důrazu na jednu či více vlastností podle přání uživatele. Z vrcholu diagramu je možné postupovat po spojnicích podle toho, zda je za nejdůležitější požadována vlastnost uvedená v uzlech diagramu o hladinu níž. Postupným přesunem k uzlům v nižších vrstvách grafu se zužuje množství objektů s požadovanými vlastnostmi.

Tabulka 7. Koncepty výsledku dotazu při hledání vhodných lyžařských středisek

Navigace v odpovědi

Vytvořený konceptuální svaz umožňuje nabídnout uživateli novou možnost při jeho další práci se sadou objektů, které tvoří výsledek prostorového dotazu. Nabídka spočívá v postupném přiblížení se k "ideálnímu" objektu z hlediska konkrétního uživatele.

Nalezené koncepty zaručují, že při volbě kterékoliv kritéria je zajištěn postup po odpovídající hraně Hasseova diagramu, jak již bylo uvedeno výše. Postupné přesouvání při zpřesňování požadavků uživatele nakonec vede k optimální volbě konkrétního objektu, přičemž pro různé uživatele se toto optimum může značně lišit.

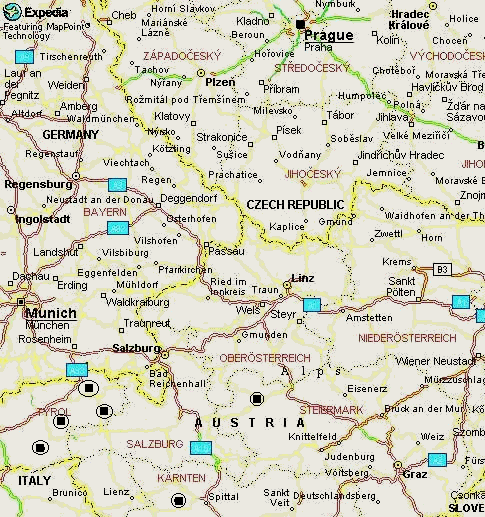
Obrázek 3. Mapa s "ideálním" střediskem.

Obrázek 4. Hasse diagram konceptuálního svazu uspořádaných lyžařských středisek.

Ukažme si nyní použití uspořádání výsledku. Předpokládejme, že nejdůležitějším požadavkem je dostatečné vybavení střediska větším počtem vleků - vybereme vrchol označený skipas. Všechny vrcholy, které patří k jeho následníkům budou tento požadavek splňovat. V mapě vybraný požadavek povede ke zvýraznění středisek s danou vlastností. V našem případě je to Mayerhofen, Kitzbühl, Söll a Gosau. Dále si uživatel zvolí další požadavek - možnost plavání ve středisku. Počet středisek klesne o jedno - v Söll není možnost si jít zaplavat.

Další zúžení povede k volbě mezi nejdelší cestou nebo nejníže umístěnými středisky. V případě, že nebudeme přikládat velkou váhu financím za několik desítek kilometrů navíc (nezapomeňme, že to bude zhruba 10% z požadovaných 500 kilometrů), dostaneme se k vrcholu, který splňuje dva požadavky úplně (skipas, bazén) a z hlediska hodnocení nadmořské výšky patří k nejvýše položeným, jen co se týče vzdálenosti patří k těm nejdále položeným.

Adeptem na nejvhodnější lyžařské středisko, splňující výše uvedená kritéria, se tedy jeví Mayerhofen označený ve výše uvedené mapě červeně.

Závěr

V článku jsme prezentovali možnosti, které nabízí použití formálního matematického aparátu založeného na teorii konceptuálních svazů. Podíváme-li se na to, co nám tato teorie nabízí, je toho velmi mnoho. Za nejzajímavější je možné považovat:

• Vytvoření hierarchické struktury odpovědi. Většina systémů používaných v současné době dává odpověď lineárně uspořádanou podle nějaké váhy, což je pro rozsáhlé systémy nevyhovující.
• Návod jak rozkládat strukturu na jednodušší části a jak redukovat složitou hierarchickou strukturu.
• Doposud známé metody pro vytváření hierarchické struktury odpovědi používají různé heuristické metody, které neumožňují provádět rozklad takto vzniklé struktury na základě nějaké sofistikované metody a tím dopředu zaručit vlastnosti takového rozkladu.

Tyto vlastnosti umožňují realizovat jednoduchou navigaci v hierarchicky uspořádané odpovědi. V další práci se chceme zaměřit na vizualizaci výsledků navigace.

Literatura

1. H. C. Arents, W. F. L. Bogaerts. Concept-based indexing and retrieval of hypermedia information. In Encyclopedia of Library and Information Science, Vol 58, Academic Press, New York 1996, 1-29.
2. L. Beran. Svazy a grupy. SNTL 1974.
3. B. Ganter, R. Wille. Formal Concept Analysis, Mathematical Foundation. Springer Verlag 1999.
4. Idrisi. Idrisi Guide to GIS and Image Processing: volume 2 http://www.clarklabs.org/
5. A. Juozapavičius, R. E. Blake. Indices and Data Structures in Information Systems. Informatica (Vilnius), 1999, Vol 10, No 1, 71-88.
6. GE Smallworld. http://www.smallworld.co.uk/english/products/utilities/networkengine
7. ering.asp
8. G. Snelting, F. Tip. Reengineering Class Hierarchies Using Concept Analysis. IBM report RC21164(94592)21APR97, 1997.
9. G. Snelting. Reengineering of Configurations Based on Mathematical Concept Analysis. ACM Transactions on Software Engineering and Methodology, 5(2):146-186, April 1996.
10. V. Snášel. Konceptuální svazy. DATESO'2001, ISBN 80-01-02376-1, 33-37.
11. http://www.mathematik.tu-darmstadt.de/ags/ag1/Literatur /liste_intern_en.html
12. R. Wille. Restructuring lattice theory: an approach based on hierarchies of concepts. In: I.Rival (ed.): Ordered sets. Reidel, Dordrecht-Boston, 445-470. 1982
13. V. Snášel. D.Ďuráková. Hierarchické uspořádání výsledků prostorového dotazu. Datakon 2001, ISBN 80-227-1597-2, Bratislava 2001.

Recenzoval: Dr. Ing. Jiří Horák (VŠB - TU Ostrava)