RNDr. Tomáš Vaníček, PhD.
Ing. Jiří Urban
Ing. Lucie Vaníčkova
Stavební fakulta ČVUT Praha
katedra inženýrské informatiky
telefon : 224354509
E - mail: vanicek@fsv.cvut.cz
Digital Terrain Model is a programme equipment for terrain reliéf describing as 3D model form. DMT is available to provide some operations by this model. The basic activities that the programmes usually are available to provide can be distributed to several sections:
1 DMT date extraction
2 DMT constructing
3 DMT browsing
4 Interpolation on the model
5 Editing of terrain and modelling
Not only a terrain relief itself compose a cultural landscape but also some more components. The landscape layout is influenced by buildings and areas for various purposes (fields, meadows, ponds). We must use other computer modelling tools and join together results from different methods to be able to model any landscapes.
The raster model is the easiest type of DMT. A terrain relief is described by array of vertical coordinates of points. The points are located in a regular raster. Raster model data usually is not taken by right measuring in a landscape but by interpolation of points measured in a nonregular raster.
The polyhedry model is the next type of DMT. For polyhedry model a landscape is parceled in smaller plane areas. Usually triangles, quadrangles so as to adjoin to a terrain relief to the nines. The terrain relief is replaced by regular polyhedron with triangle or quadrangle faces.
The plate model has many attributes alike the polyhedry model. A terrain is parceled smaller areas. No only plane ones. They can be anyway curved. Most frequently used areas are ones describable by polynomical functions what to continue one another enough fluently that there is warranted derivatives continuity up to default a order.
The plate model is constructed gradually by several steps. The first step is a triangulation. It is merging a input index of points to a triangle net. Such triangle net can be constructed by many way. Some of the way are more available for next operations that others ones. A result of the triangulation is the terrain model described by a available data structure. A member of terrain model construction can be optimization of single plates. Needless edges of triangle net are cut out during the optimization. Then the model is composed quadrangles and more compound polygons.
The last phases of the model creation is treatment singularities. The singularity is a place, where a terrain goes on different way as it is expected from going on a around of the singularity. E.g. it can be an edgy ridge or a coast of a lake.
A lot of theoretical problems rises during a creation of the plate model. The first of them is the triangulation itself. An effectiveness of whole programme package for the terrain and landscape digital model is highly influenced by triangulation algorithm effectiveness just. This algorithm must be enough fast and withal offer a good duality of triangulation.
The next problem is curvature of the Terezin plates so as to continue one another fluently. This problem is missed
in a many commercial programmes. Because a visual image is the most important for a practical work. Sometimes approx fluently kontinuity of the polyhedry plates is enough. Another time fluently kontinuity of the plates specially polyhedry ones with various numbers of apexes is a large theoretical problem.
The last set of problems is a treatment of singularities. There are different types or the singularities. Sometimes we can apply for some edges a fluently continuity a terrain itself but no fluently continuity of the plates (derivatives continuity). E.g. ridge. Sometimes neither terrain itself as a function of two variables (hight Z is assigned to position coordinates X and Y) do not have to be continuous. The terrain can include a break (a vertical brow what two plates do not continue fluently on), or even a cornice (a place what two plates overlap partly and the terrain does not make a function). Because the types of singularities (break, cornice) affect rather rarely and their programme treatment is very difficult, a lot of programmes for DMT go about a those singularities solving. The break is often realized by a plummeting plate what to be still a graph of a function of two variables. A plummeting brow appears instead of a vertical brow in a resultant model.
The staffs team of the department of informatics, college of civil engineering, Czech Technical University, Prague,
deals with DMT more 15 years. A lot of the indicated theoretical problems were resolved and their resolution was tried in practice, others problems wait for a complex resolutions.
Digitálním modelem terénu (dále DMT) se obvykle rozumí programový prostředek sloužící k popisu terénního reliéfu ve formě třírozměrného modelu a k provádění jistých operací s tímto modelem. Základní činnosti, které programy pro digitální model terénu obvykle umožňují vykonávat, lze rozdělit do několika oblastí:
1. Získávání údajů o terénním reliéfu.
2. Vlastní tvorba terénního modelu. 3. Prohlížení terénního modelu.
4. Výpočty prováděné na DMT.
5. Úpravy terénu a modelování.
Kulturní krajinu spoluvytváří nejen vlastní terénní reliéf, ale i další složky. Vzhled krajiny podstatně ovlivňují stavby (silnice, domy), či plochy využívané k určitým účelům (pole, louky, rybníky). Abychom mohli modelovat krajinu ve vší obecnosti, je potřeba využívat i další prostředky pro počítačové modelování a hlavně mít možnost spojovat výsledky získané různými metodami.
Nejjednodušším typem DMT je model rastrový. Terénní reliéf je popsán maticí výškových souřadnic bodů rozmístěných v pravidelném rastru. Data pro rastrový model nejsou obvykle získávána přímo měřením v terénu, ale interpolací bodů naměřených v rastru nepravidelném.
Dalším typem terénního modelu je model polyedrický. Při jeho použití je terén rozdělen na menší rovinné plošky, obvykle na trojúhelníky či čtyřúhelníky tak, aby se tyto plošky co nejlépe přimykaly k reliéfu terénu. Terénní reliéf je pak vlastně nahrazen pravidelným mnohostěn s trojúhelníkovými či čtyřúhelníkovými stěnami.
Plátový model má mnoho rysů společných s modelem polyedrickým. Terén je opět rozdělen na menší plošky, které však nemusí být pouze rovinné, mohou být i jistým způsobem zakřivené. Nejčastěji se používají plochy popsatelné polynomickými funkcemi, které na sebe při hraničních liniích navazují natolik hladce, aby byla zaručena spojitost derivací do jistého předem daného řádu.
Tvorba plátového modelu ze vstupních dat postupuje v několika krocích. Prvním krokem je triangulace, tedy pospojování vstupního seznamu bodů do trojúhelníkové sítě. Takovou trojúhelníkovou síť lze vytvořit mnoha různými způsoby, z nichž některé jsou pro další práci vhodné více a jiné méně. Výsledkem triangulace je terénní model popsaný vhodnou datovou strukturou. Součástí tvorby modelu může být i optimalizace jednotlivých plátů. Při ní jsou některé zbytečné hrany trojúhelníkové sítě vypuštěny a model je pak tvořen i čtyřúhelníky, či ještě složitějšími mnohoúhelníky.
Poslední fází tvorby modelu je ošetření singularit. Singularitou rozumíme místo, kde se terén chová jiným způsobem, než by se dalo usoudit z jeho chování v okolí singularity. Typicky se může jednat například o ostrý horský hřeben, nebo pobřežní linii jezera.
Během tvorby plátového modelu terénu vzniká celá řada teoretických problémů. Prvním z nich je samotná triangulace. Efektivitu celého programového balíku pro digitální modelování terénu a krajiny totiž významně ovlivňuje právě efektivita triangulačního algoritmus. Tento algoritmus musí být dostatečně rychlý a přitom musí poskytovat triangulaci dobré kvality.
Dalším problémem je zaoblování terénních plátů tak, aby na sebe hladce navazovaly. Tento problém je v mnoha komerčních programech pominut, neboť pro praktickou práci je nejdůležitější vizuální dojem, a pro něj leckdy stačí pouze "přibližně hladké navázání polyedrických plátů. Jinak je ovšem hladké navázání plátů zvláště v případě polyedrů s různým počtem vrcholů velkým teoretickým problémem.
Poslední sadou problémů je ošetření singularit. Singularity mohou být opět různých typů. Na některých hranách například můžeme požadovat spojitost vlastního terénu, ale nikoliv již hladké napojení plátů (spojitost derivací). Příkladem může být horský hřeben. Někdy ani samotný terén chápaný jako funkce dvou proměnných (k polohopisným souřadnicím x a y je přiřazena výška z) nemusí být spojitý. Terén může obsahovat zlom (tedy kolmý sráz, na kterém na sebe dva pláty nenavazují spojitě), nebo dokonce převis (místo, kde se dva pláty částečně překrývají a terén tedy netvoří funkci). Jelikož singularity těchto druhů (zlom, převis) se vyskytují poměrně zřídka a jejich programové ošetření je dosti náročné, řada programů pro DMT řešení takových singularit obchází. Často je například zlom realizován prudce klesajícím plátem, který je však stále ještě grafem funkce dvou proměnných. Místo kolmého srázu se tedy ve výsledném modelu objeví velmi prudce klesající svah.
Kolektiv pracovníků Katedry inženýrské informatiky Stavební fakulty ČVUT v Praze se digitálním modelováním terénu zabývá již více než 15 let. Mnohé z naznačených teoretických problémů jsme vyřešili a jejich řešení i odzkoušeli v praxi, jiné problémy na komplexní řešení ještě čekají.
Digitálním modelem terénu (DMT) se většinou rozumí geometrický popis reliéfu terénu. Na modelu terénu lze potom dále modelovat a popisovat nejrůznější informace, jak je tomu například u topografických map. Tedy umístění přírodních i umělých objektů, hranice správních celků, hranice povodí atd. Takové informace jsou však z pohledu klasického pojetí digitálního modelu terénu méně důležité a hlavně svým charakterem velmi komplikují orientaci používaných systémů na čistou prostorovou geometrii reliéfu terénu. Geometrie terénu má totiž velmi charakteristické prvky, které předurčují většinu současných programových systémů k tomu, aby zpracovávaly pouze ji. Charakteristické prvky jsou především tyto:
1. Terénní plocha je velmi nepravidelná. Vykazuje místa, kde je průběh hladký, jinde jsou linie, na kterých je hladkost narušena. Dokonce se lze setkat s terénními stupni, které jsou sice většinou umělé, nicméně k terénu patří. Zvláštní charakter mají také vrcholy, sedla, údolnice a hřbetnice, které mají podélně často hladký průběh, ovšem v kolmém směru se na nich terénní plocha může ostře lámat. Tyto jevy se v terminologii DMT nazývají singularity, jejich matematickou charakteristikou je nespojitost funkce či nespojitost její derivace.
2. Modelovaná plocha může být velmi rozsáhlá, popisovaná značným počtem dat. Na druhé straně vzhledem k rozsáhlosti většinou dosahuje malých převýšení, rozměry ve směru os x a y jsou větší než ve směru osy z.
3. Valnou většinu terénních ploch lze charakterizovat jako funkci polohopisných souřadnic x, y. Těm lze totiž vždy přiřadit pouze jednu výškovou složku z. Výjimkou mohou být terénní stupně (zlomy nebo též schody), ve kterých je terénní plocha svislá, někdy dosahuje až charakteru převisu. Tzv. převisy jsou místa, kterými lze vést svislici, protínající povrch ve dvou nebo více bodech. Taková místa se vyskytují velmi zřídka a pro potřeby modelování terénu nemají velký význam. Ovšem v případě jejich zpracování vyvstává velký problém, jakým komerčním produktem převisy řešit, neboť systémů, vhodných pro zpracování rozsáhlých DMT a schopných zohlednit takové detaily, je pomálu.
Problematika zpracování digitálního modelu terénu (DMT) zasahuje do dvou disciplín - mezi systémy CAD (objemové modelování, zobrazování) a mezi GIS systémy (rozsáhlostí dat a shodným předmětem modelování). Jedná se však o samostatnou problematiku, kterou je nutné chápat izolovaně.
Pro inženýrské úlohy je důležité vybrat správnou kategorii software (CAD, GIS, DMT), z nichž každý může být orientován na stejný předmět (krajinu, terén), ovšem s různými rozlišovacími schopnostmi. Při podrobném modelování rodinného domu použijeme jistě CAD systém (především jeho objemový modelář). Pokud chceme vymodelovat urbanistický celek (vesnici), nezajímají nás již konstrukční detaily každého domu, zato počet domů vzroste. Použijeme program pro DMT, který schematicky zobrazí stavby, k nim přidá terén a vytvoří tak celou krajinnou scenérii. Pokud se budeme zajímat o vyšší územní celky, zajímá nás většinou pouze polohopis (výškopis maximálně schematicky - přes nakreslené vrstevnice) a dále vedení inženýrských sítí, silnice, řeky, hranice, pozemky atd. Použijeme tedy GIS. Vše je otázkou rozlišovací úrovně či stupně generalizace.
Pro snadný popis terénu se většinou používá princip rozdělení celé plochy na menší části, které se dají snadněji geometricky popsat. Podle charakteristik těchto plošek se rozlišují následující typy modelů:
Polyedrický: Zde jsou elementárními ploškami trojúhelníky, které k sobě přiléhají. Doplníme-li plošky o stěny na obvodu celého modelu (sokl) a o podstavu, získáme mnohostěn, přimykající se k terénu. Vrcholy mnohostěnu jsou body na terénní ploše, souřadnicově určené příslušnými geodetickými metodami. Interpolace plochy se obvykle provádí lineárně po trojúhelnících. Tento přístup je v současné době u komerčních systémů nejrozšířenější. Vrcholy trojúhelníků je vhodné zvolit tak, aby vystihovaly nejen obecně průběh terénu, ale i jeho singularity.
Plátový: Tento typ modelu předpokládá, že se povrch rozdělí na nepravidelné, obecně křivé plošky trojúhelníkového nebo čtyřúhelníkového tvaru, přičemž hranice dělení se vedou po singularitách. Pro popis jednotlivých plošek se obvykle používají polynomické funkce. Stupeň těchto funkcí souvisí se stupněm hladkosti navázání jednotlivých plátů. Rozdělení modelu na pláty je velmi výhodné a snadné je rozdělení vést po singularitách charakteristických bodech terénu.
Rastrový: Jak název napovídá, model je dán množinou elementárních plošek nad prvky pravidelného rastru. Obvykle jsou to čtyřúhelníky, které je případně možno rozdělit na trojúhelníky, nebo spoji do složitějších ploch. Pro popis jednotlivých plošek pak postačuje funkce, která je součinem dvou lineárních funkcí jedné proměnné.
Rastrový model je výhodný v tom, že se pracuje s pravidelnou maticí uzlových bodů, které se dají snadno vypočítat a není nutné o nich udržovat všechna data. Ovšem vypovídací schopnost modelu silně závisí na jeho rozlišovací úrovni, nakolik jsou jednotlivé prvky rastru přimknuty ke skutečnému reliéfu terénu. Velmi špatně se taková hustota volí pro krajinu s velkou nepravidelností, kde jsou vysoké hory i rozsáhlé rovné pláně nebo jezera. Takový reliéf je nutné řešit rozdělením na několik modelů a každý zpracovávat v různém rozlišení.
Rastrový model je v principu definován hodnotami [x, y, z] - tedy prostorovými souřadnicemi každého bodu rastru. Při praktickém použití stačí určit vzdálenost bodů rastru a umístit jeden bod do souřadného systému, všechny ostatní prvky rastru se dají dopočítat. Proto může obsahovat prakticky použitelný rastrový formát pouze:
- souřadnice jednoho rohu rastru,
- úhel natočení rastrové sítě
- rozměr jednoho prvku (oka) rastru,
- matici výškových hodnot každého bodu rastru.
Pro datovou reprezentaci terénního modelu jsou vhodné různé datové struktury, které především odrážejí charakter právě popsaných typů modelů. Pro polyedrický a plátový model je velmi vhodné použít strukturu "okřídlená hrana".
Konstrukce nepravidelné trojúhelníkové sítě (triangulace) je zásadním nástrojem při vytváření polyedrického nebo plátového modelu, který používá většina systémů DMT.
Vstupními daty je množina bodů P1,P2,P3,...,Pn, které jsou dány svými
prostorovými souřadnicemi [x, y, z]. Vrcholy je nutné pospojovat hranami tak, aby vznikla množina trojúhelníků, které k sobě přiléhají a neprotínají se. Tyto trojúhelníky se musí maximální mírou přimykat k aproximované ploše reliéfu terénu. Zásadní charakteristikou algoritmu pro tvorbu sítě tedy je, které vlastnosti považuje za určující při optimalizaci maximálního přimykání sítě k aproximované ploše a jakou mírou dokáží tuto jinak značně časově náročnou činnost urychlit.
Problematika tvorby trojúhelníkové sítě je velmi zajímavá a není stále v žádném profesionálním systému dovedena k dokonalosti. Některé základní typy algoritmů ukazují známé způsoby tvorby sítě. Vstupem je vždy množina bodů
P1(x1,y1,z1), P2(x2,y2,z2), P3(x3,y3,z3), ..., Pn(xn,yn,zn).
Výstupem z triangulačního algoritmu je množina úseček, M subset { PiPj | i < j } splňujících následující vlastnosti:
1. Žádné dvě úsečky nemají společný žádný vnitřní bod.
2. K množině M nelze přidat žádnou další úsečku, aniž by se tím porušila podmínka 1.
Lze dokázat, že plochy ohraničené úsečkami z množiny M jsou trojúhelníky (jedinou výjimkou je "vnější plocha" vně konvexního obalu množiny bodů P1, P2, ... , Pn .
Mezi přípustnými triangulacemi nás obvykle budou zajímat triangulace, které v jistém kritériu prokazují dobré, nebo dokonce optimální hodnoty. Toto formalizované kritérium by mělo nahradit neformální požadavek, aby "trojúhelníky dobře přimykaly k terénu". Kritériem optimality může být například součet délek všech úseček z množiny M. Následující tři algoritmy generují triangulace optimální z hlediska tohoto kritéria:
Algoritmus 1.:
1. vytvoř všechny možné spojnice bodů z množiny P a dej je do množiny M.
2. pro každou spojnici z množiny M proveď: pokud svojí délkou přesahuje povolenou mez, zruš ji pokud přetíná spojnici kratší,zruš ji
3. výsledkem je množina M, obsahující triangulaci
Algoritmus 2.:
1. vytvoř všechny možné spojnice bodů z množiny P a dej je do množiny K.
2. srovnej spojnice v množině K podle délky od nejkratší po nejdelší.
3. vezmi nejkratší spojnici z množiny K a přemísti ji do množiny M.
4. pokud v množině K nezbude žádná spojnice, algoritmus končí a v množině M je hledaná triangulace
5. vezmi nejkratší spojnici z množiny K a proveď:
pokud přetíná tato spojnice některou stávající spojnici v množině M, tak:
zruš ji
jinak:
přemísti ji do množiny M.
6. pokračuj krokem 4.
Algoritmus 3.:
1. jakýmkoliv náhodným způsobem vytvoř jakkoli špatnou trojúhelníkovou síť K (např. vezmi jeden bod za střed, spoj ho se všemi ostatními body sítě a nakonec pospojuj body po obvodě sítě.)
2. Opakuj body 3 a 4, dokud během jejich provádění dochází k nějakým změnám množiny K.
3. Opakuj bod 4 pro všechny úsečky AB z množiny K.
4. Vezmi úsečku AB a najdi k ní přilehlé trojúhelníky ABC a ADB. Je-li délka úsečky CD menší než délka úsečky AB, vyřaď AB z množiny K a zařaď do ní CD.
Uvedené algoritmy mají pochopitelně různou časovou složitost. Algoritmus 3 je nejefektivnější. Podrobný rozbor časových složitostí jednotlivých algoritmů je uveden například v [1].
Následující algoritmus generuje trojúhelníkovou síť, jejíž průmět do vodorovné roviny splňuje tzv. Delenayuvu podmínku. Vnitřek kruhu opsaného libovolnému z trojúhelníků
sítě neobsahuje žádný bod sítě. Při použití vhodných datových struktur pracuje tento algoritmus v čase lineárně závislém na počtu bodů a je tedy podstatně efektivnější než všechny výše uvedené algoritmy.
Algoritmus 4.:
1. Zvol libovolný počáteční bod A (nejlépe přibližně uprostřed množiny bodů P).
2. Najdi bod B nejbližší k bodu A, zařaď úsečku AB do množiny K a orientované úsečky AB a BA do seznamu orientovaných úseček S.
3. Je-li seznam S prázdný, ukonči práci, jinak opakuj body 4-6.
4. Vezmi poslední úsečku seznamu S (nazveme ji AB) a najdi bod C takový, aby úhel ACB byl maximální.
5. Pokud bod C není incidentní se žádnou úsečkou z množiny K, zařaď do množiny K úsečky AC a BC a do seznamu S úsečky AC a CB.
6. Pokud bod C je incidentní s nějakou úsečkou množiny K, je nutné vyřešit konfliktní situace a zařadit do množiny K a do seznamu S vhodné úsečky, tak aby seznam stále obsahoval úsečky ležící na obvodu "dosud pospojované" oblasti.
Incidencí se v posledním algoritmu rozumí vztah dvou útvarů (v našem případě bodu a úsečky), při kterém jeden útvar obsahuje druhý nebo s ním má společnou nějakou část. V konkrétním případě incidence znamená, že bod C je krajním bodem úsečky.
Výše uvedené algoritmy jsou pro názornost značně zjednodušené a především neobsahují jednu důležitou složku - možnost včlenit tzv. předurčené hrany. Předurčené nebo také předdefinované či pevné hrany jsou takové spojnice bodů, pomocí kterých si uživatel vyžádá již ve vstupu (současně se zadáním množiny bodů) spojení vybraných bodů, které považuje za definitivní. Jsou to většinou singularity a podobná charakteristická místa terénu, na kterých by
algoritmus mohl vytvořit triangulaci jinak, než požaduje uživatel.
V obecných případech vznikne z každého popsaného algoritmu jiná trojúhelníková síť, algoritmy mohou úsečkami spojit jiné body. Rozdíly zřejmě nikdy nebudou zásadní, často vzniknou zcela shodné výsledky, nicméně nelze na to spoléhat.
Některým systémům, pracujícím s hrubým modelem terénu, stačí vytvořený polyedrický model, složený z rovinných trojúhelníků. Pro větší přesnost je však vhodné trojúhelníkovou síť dále upravit. Především je možné některé hrany vypustit a zpracovávat dále kromě trojúhelníků také čtyřúhelníky nebo obecné n-úhelníky. Ty mohou být zborcené v případě, že mají opisovat nějaké "ostrůvky" v terénu, ve kterých je např. zasazen stavební objekt nebo podobně. Pro přesný popis reliéfu je nutné tyto n-úhelníky zaoblit a vytvořit z nich křivé plošné elementy.
Nejčastěji používanou metodou pro zaoblování je tzv. Coonsova plocha. Coonsovy plochy je vhodné použít pro plátový model, ve kterém jsou všechny pláty tvořeny trojúhelníky. Coonsova plocha je plocha kvadratická, tedy plocha, kterou lze vyjádřit implicitní rovnicí:
R1: z = ax2 + by2 + cxy + dx + ey + g
a která splňuje následující dvě podmínky:
- Plocha prochází všemi třemi krajními body trojúhelníkového plátu.
- Na rozhraní dvou plátů je spojitá alespoň první derivace terénu. Přesněji řečeno, funkce jedné proměnné ![]() , která vznikne jako funkce nadmořská výška podél libovolné spojité trajektorie přecházející z jednoho plátu na druhý, má spojitou první derivaci.
, která vznikne jako funkce nadmořská výška podél libovolné spojité trajektorie přecházející z jednoho plátu na druhý, má spojitou první derivaci.
Uvedené dvě podmínky dávají 6 rovnic (3x pro incidenci bodů a 3x pro rovnost derivací zleva a zprava v krajních bodech plátu). Pomocí nich lze vypočítat 6 parametrů Coonsovy plochy (a,b,c,d,e,g).
Praxe však ukazuje, že často je vhodné použít kromě plátů trojúhelníkových i pláty s větším počtem vrcholů, například čtyřúhelníkové. Zvláště typické je použití čtyřúhelníkových plátů při modelování průchodu liniových staveb terénem. Problém
hladkého navazování čtyřúhelníkových plátů, stejně tak jako problém navázání plátu čtyřúhelníkového a trojúhelníkového je v oboru kvadratických ploch neřešitelný. Je zde totiž více než 6 podmínek, které musí daná kvadratická plocha splňovat ale jen 6 koeficientů, které tvar plochy ovlivňují.
Vzniká tedy teoretický problém, jak pláty větší než trojúhelníkové na sebe navázat, když už ne zcela hladce, tak "co nejblíže" hladkosti. Matematicky řečeno to znamená tak, aby se rozdíl pravé a levé derivace nadmořské výšky podle libovolné trajektorie v krajních bodech plátu blížil 0.
V případě čtyřúhelníkových plátů je navíc potřeba dodržet 4 podmínky pro incidenci vrcholů plátu. Proto lze 4 koeficienty kvadratické plochy (například a,b,c,d) vyjádřit pomocí ostatních dvou (e,g). Koeficienty e a g je pak potřeba stanovit takové, aby se rozdíly derivací na všech čtyřech stranách plátu co nejvíce blížily 0 a plát tak na své okolí navazoval co možná nejhladčeji.
Jedním z možných způsobů optimalizace co nejvíce hladkého napojení plátů je použití evolučních výpočetních technik (EVT). Použijeme genetické algoritmy (GA) pro nalezení co nejoptimálnějšího zaoblení čtyřúhelníkových ploch.
Po dosazení čtyř zadaných krajních bodů plátu (jejich souřadnic x, y, z) do rovnice R1, dostaneme čtyři rovnice o šesti proměnných:
R2: z1 = ax12 + by12 + cx1y1 + dx1 + ey1 + g
R3: z2 = ax22 + by22 + cx2y2 + dx2 + ey2 + g
R4: z3 = ax32 + by32 + cx3y3 + dx3 + ey3 + g
R5: z4 = ax42 + by42 + cx4y4 + dx4 + ey4 + g
Z rovnic R1-R4 vyjádříme proměnné a,b,c,d a dosadíme do čtyř rozdílů pravé a levé derivace na všech čtyřech stranách plátu. Dostaneme čtyři rovnice o dvou proměnných:
R6: f1(e,g)=0
R7: f2(e,g)=0
R8: f3(e,g)=0
R9: f4(e,g)=0
My potřebujeme nalézt takové hodnoty e a g, pro které budou mít všechny čtyři funkce hodnoty blížící se co nejvíce k nule:
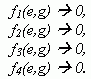
Hledáme tedy minima jejich absolutních hodnot:
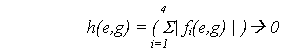
Na nalezení optimálních e a g použijeme genetický algoritmus: budeme generovat e a g tak, abychom dospěli k minimům funkce h(e,g).
Takhle vygenerujeme velké množství plátů a z nich pak budeme vybírat na základě nějakých kritérií jeden plát.
Obecně lze základní GA popsat takto:
V takovém GA mají nadprůměrní jedinci větší šanci na ovlivnění další populace než podprůměrní. Proto vznikne lepší populace, než byla původní. Pro výběr jedinců z jedné populace do následující lze použít různé metody, potom se mohou např. silnější jedinci promítnout do další generace víckrát a nejslabší vůbec.
Při tvorbě GA pro vygenerování plátů, z nichž si vybereme jeden vyhovující plát, se budeme potýkat s následujícími problémy:
1. Najít vhodnou reprezentaci proměnných e,g.
2. Použít vhodný a výkonný operátor křížení.
3. Použít efektivní způsob výběru jedinců z populace.
4. Nastavit pravděpodobnost křížení a mutace jedinců.
5. Určit zastavovací pravidlo nebo počet průchodů GA.
6. Určit systém sestavování nové generace (kolik původních jedinců a kteří se do ní dostanou).
7. Vygenerování startovací populace (lze už nějak optimalizovat).
8. Po vyřešení problémů 1-7 sestavit efektivní GA.
Při výběru nejvhodnějšího jedince z množiny vygenerovaných plátů budeme postupovat na základě určených kritérií. Kritéria určíme tak, abychom vybrali "nejhladší" plát. Vybereme plát s minimální funkcí h takový, aby f1, f2, f3 i f4 se blížily nule (tzn. plát bude co nejlépe navazovat na všechny čtyři sousední pláty):
1. Vybereme plát s minimální h(e,g), tzn. nejoptimálnější plát z vygenerovaných jedinců, který bude splňovat podmínku 2.
2. Vybraný plát musí splňovat:
![]() R určíme na základě experimentů.
R určíme na základě experimentů.
Vygenerování DMT
Algoritmy pro hledání jednotlivých plátů musí být efektivní, tzn. že jejich výpočetní náročnost a celková délka (závisející i na počtu proběhnutí GA) nesmí být přehnaná, aby celé vygenerování DMT proběhlo v rozumném čase. Optimální GA s optimálními nastaveními bude nalezen pomocí experimentů.
Poslední sadou problémů, které je obvykle nutné řešit současně se zaoblováním plátů, je ošetření singularit. Singularitou rozumíme místo, kde se terén chová jiným způsobem, než by se dalo usoudit z jeho chování v okolí singularity. Typicky se může jednat například o ostrý horský hřeben, nebo pobřežní linii jezera.
Singularity mohou být opět různých typů. Na některých hranách například můžeme požadovat spojitost vlastního terénu, ale nikoliv již hladké napojení plátů (spojitost derivací). Příkladem může být horský hřeben. Někdy ani samotný terén chápaný jako funkce dvou proměnných (k polohopisným souřadnicím x a y je přiřazena výška z) nemusí být spojitý. Terén může obsahovat zlom (tedy kolmý sráz, na kterém na sebe dva pláty nenavazují spojitě), nebo dokonce převis (místo, kde se dva pláty částečně překrývají a terén tedy netvoří funkci). Jelikož singularity těchto druhů (zlom, převis) se vyskytují poměrně zřídka a jejich programové ošetření je dosti náročné, řada programů pro DMT řešení takových singularit obchází. Často je například zlom realizován prudce klesajícím plátem, který je však stále ještě grafem funkce dvou proměnných. Místo kolmého srázu se tedy ve výsledném modelu objeví velmi prudce klesající svah.
Náš návrh klasifikace singularit sice neumožňuje vyjádřit libovolnou singularitu (to ani z principu není možné), ukazuje se však, že většinu reálných situací, které se v přirozené i v kulturní krajině vyskytují, lze do naší klasifikace zahrnout.
Všechny singularity budeme považovat za liniové a budeme je tedy vyjadřovat pomocí předurčených hran. K předurčeným hranám musí již přihlížet triangulační algoritmus a musí je zařadit do modelu. Při zaoblování je pak potřeba příslušně upravit použité zaoblovací vzorce a postupy.
Předurčenou hranu klasifikujeme podle dvou hledisek:
1) Tvar hrany
1. Úsečka
2. Křivka ve vertikální rovině
3. Obecná křivka
2) Způsob navázání plátů
1. Hladké navázání (spojitost terénu i jeho první derivace)
2. Ostré navázání (terén spojitý, jeho derivace nespojitá)
3. Zlom (terén nespojitý)
Kombinací výše uvedených klasifikací pak vznikne celkem 9 typů singularit. Třeba poznamenat, že singularita typu 3,1 (obecná křivka, hladké navázání plátů) vlastně žádnou singularitou není, neboť v tomto případě bude terén zpracováván stejným způsobem jako při běžném zaoblování. Typů singularit je tedy ve skutečnosti jen 8.
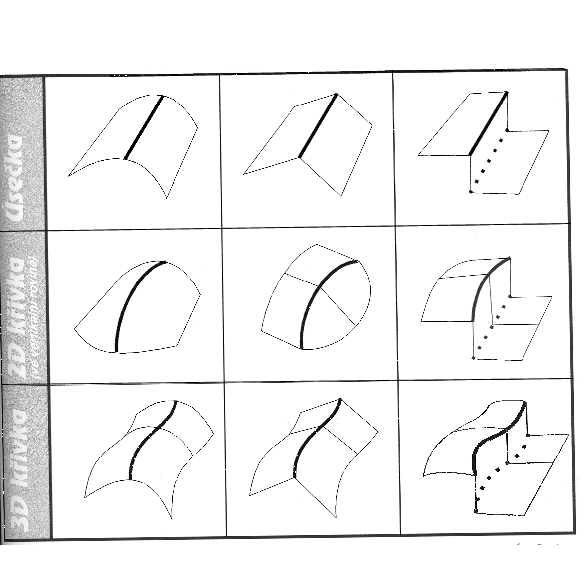
Obr č. 1 Typy singularit
Většina uvedených teoretických postupů byla pracovníky a studenty KII FSv ČVUT použita při programování školního digitálního modelu terénu TOPOS. Tento program je pro nekomerční účely zdarma k dispozici u autorů článku, většiny algoritmů i programu.